
■第一节事故树分析概述
1 .概述
■①事故树分析(Fault tree analysis):又称 故障树分析,是从结果到原因找出与灾 害事故有关的各种因素之间因果关系和 逻辑关系的作图分析法。



■原因:
■第一层:可燃物(LPG);助燃物(空气 中的氧),点火源(明火、静电、摩擦 火星等)
.第二层:可燃物(LPG),泄漏
.第三层:泄漏原因:翻车拉裂气相管法 兰接口 >
.第四层:翻车原因:转弯车速过快
槽车着火
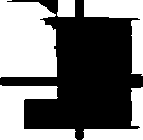
Jt____ g *
可燃物 助燃物 点火源
法兰口泄漏

*
转弯车速过快


隽特点:
♦结果:系统可能发生的事故放在图的最上面, 称为顶上事件
♦原因,可能是其他一些原因的结果,称为中间
原因事件,应继续往下分析。直到找出不能进一
步往下分析的原因为止,这些原因称为基本原因
事件。
♦图中各因果关系用不同的逻辑门联结起来,这样 得到的图形象一棵倒置的树。
油库火灾
吞
可燃物
71
氧化剂
*
明火
电火花
撞击火花
穿戴铁 钉鞋
使用铁 制工具
点火源
J 、《
静电火花 雷电火花

■ The fault tree was first developed in 1961 for the U.S. military intercontinental missile program. The U.S. Nuclear Regulatory Commission published a guide in 1981, and since then FTA has been used in almost
every engineering discipline around the would.
■事故树分析法是采用演绎方法分析事故 的因果关系,能详细找出系统各种固有 的潜在的危险因素,为安全设计、制定 安全技术措施和安全管理要点提供了依
据。
■能简洁、形象表示出事故和各种原因之 间因果关系及逻辑关系。
■在事故树分析中顶上事件可以是已发生 的事故,也可以是预想的事故。通过分 析,找出原因,釆取对策措施加以控制, 从而起到预测预防事故的作用。
■可选择最感兴趣的事故作为顶上事件分 析,这和事件树不同,事件树是由一个 故障开始,而引起的事故不一定是使用 者最感兴趣的。
■事故树分析法既可以用于定性分析,也 可以用于定量分析。通过定性分析,确 定各种危险因素对事故树影响的大小, 从而掌握和制定防灾控制要点;而定量 分析,则能计算出顶上事件发生的概率, 并可以从数量上说明危险因素的重要度, 为实现系统最佳安全目标提供依据。
■编制者应对系统非常熟悉和有丰富的经 验,并且要准确的掌握好分析方法。
■对很复杂的系统,编出的事故树很庞大, 这给定性定量分析带来一定的困难,有 时甚至连计算机都难以实现。
■要对系统进行定量分析,必须知道事故 树中各事件的故障率,如果这些数据不 准确则定量分析便不可能。
■事故树分析的程序,常因评价对象、 分析目的、粗细程度的不同而不同, 但一般可按如程进行:
熟悉系统
确定顶上事件k
调查事故
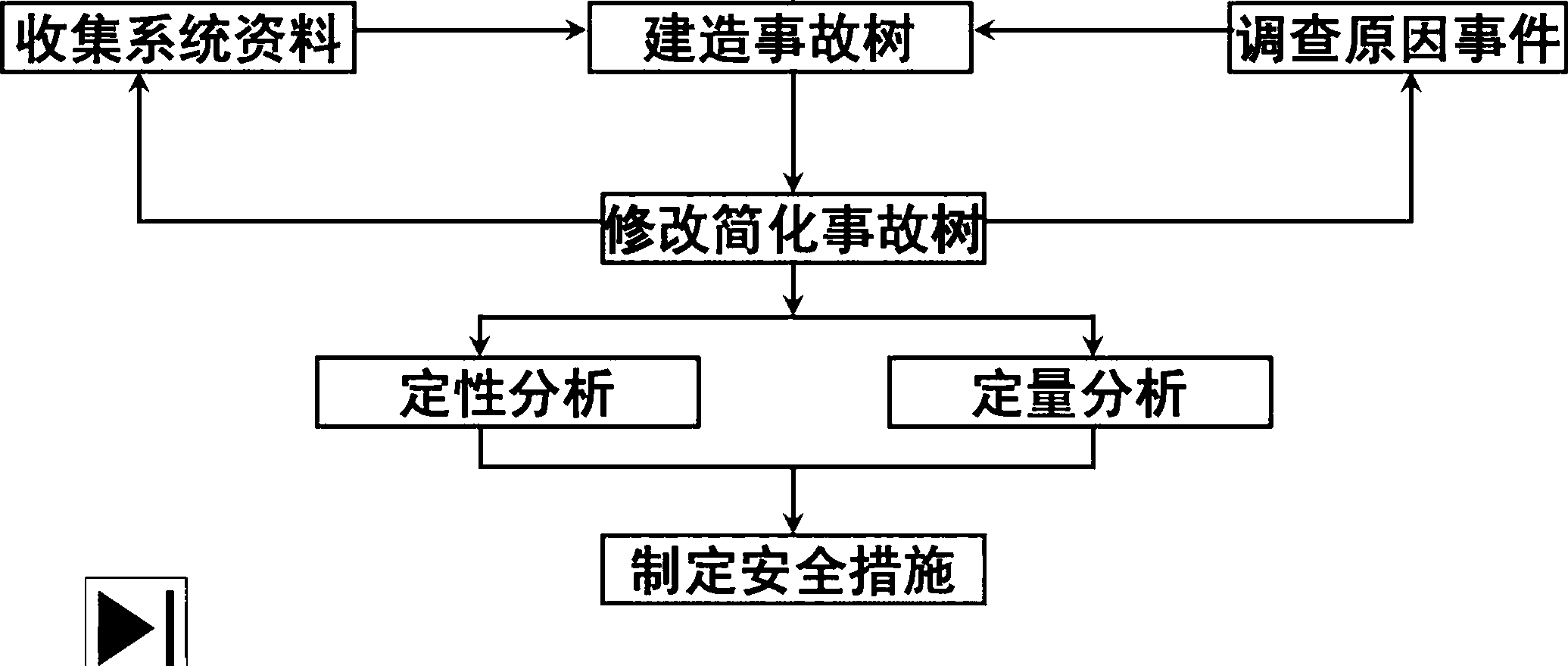
①确定和熟悉分析系统。
♦明确分析的范围和边界,包括工艺流程、 设备构造、操作条件、环境状况及控制 系统和安全装置等。
♦广泛收集系统发生过的事故。包括本单 位的事故情况、同行业类似系统或设备 以及国外事故资料,以便确定所要分析 的事故类型。
■②确定顶上事件。一般选择发生可能性 较大且能造成一定后果的那些事故作为 务析对豪。
■确定顶上事件时,要坚持一个事故编一 棵树的原则且定义明确,例如:“加氢 反应温度过高”,“氧气钢瓶超压爆 炸",象“过程火灾”,“化工厂爆炸" 这些太笼统了,无法向下分析。
③调查原因事件。就是找出系统的所有潜
在危险因素和薄弱环节,包括设备元件
等硬件故障、软件故障、人为差错以及 环境因素,凡与事故有关的原因都找出 来,作为事故树的原因事件。
④确定不予考虑的事件。与事故无关的原 因有各种各样,但有些原因根本不可能 发生或发生机会很少,如导线故障、飓
风、龙卷风等,编制事故树可不予考虑,
但要事先说明。
⑤确定分析的深度。在分析原因事件时, 要分析到哪一层为止,需事先明确。
分析的太浅,可能发生遗漏;分析得 太深,则事故树过于庞大繁琐。具体
深度应视分析对象而定。对化工生产 系统来说,一般只到泵、阀门、管道 故障为止;电器设备分析到继电器、
开关、马达故障为止,其中零件故障 就不一定展开分析。

⑥编制事故树。
丄♦从顶上事件开始,釆取演绎分析方法,逐层向 ,下找出直接原因事件,直到所有最基本的事件
为止。每一层事件都按照输入(原因)与输出 (结果)之间逻辑关系用逻辑门连接起来。这 样得到的图形就是事故树树。
♦初步编好的事故树应进行整理和简化,将多余 事件或上下两层逻辑门相同的事件去掉或合并O 如有相同的子树,可以用转移符号表示省略其 中一个,以求结构简洁、清晰。
⑦事故树定性分析。可从事故树结构上求
最小割集和最小径集,
进而得到每个基
本事件对顶上事件的影响程度,为釆取 安全措施的先后顺序、轻重缓急提供依
据。
⑧事故树定量分析。定量分析可计算出事
故发生的概率,并从数量上说明每个基
本事件对顶上事件的影响程度,从而制 定出最经济、最合理的控制事故的方案,
实现系统最佳安全的目的。
■事故树釆用的符号包括:事件符号、逻 辑门符号、转移符号三大类。
■事件分:事故事件和成功事件。
■事故事件:在事故树分析中各种非正常 状态或不正常情况称事故事件。
.成功事件:各种完好状态或正常情况称 成功事件。
* ■ (1)矩形符号。矩形符号表示顶上事件和中 间事件。顶上事件是所分析系统不希望发生的 事件。它位于事故树的顶端。中间事件是位于

■ Intermediate event 一 A fault event that occurs because of one or more antecedent causes acting through logic gates

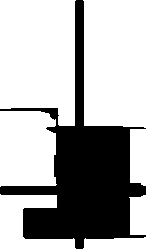
易燃液体 仓库火灾
可燃物I 氧化剂

使用铁
制工具
点火源......
莅.
|
静电火花 |
雷电火花 |
22
■ (2)圆形符号。
形符号表示基本原因
事件即基本事件,是不能再往下分析的 事件,故位于事故树的底部。
■ Basic event 一 A basic initiating fault
requiring no further development


■ (3)菱形符号。菱形符号有两种意义。一种 是表示省略事件,即没有必要详细分析或原因 不明确的事件。另一种是表示二次事件,如由 窟始废書引起的二次灾害,即来自系统之外的 蔗因事屛。
■ Undeveloped event 一 An event which is not further developed either because it is of insufficient consequence or because information is unavailable
o
■(4)房形符号。房形符号表示正常事件, 是系统正常状态下发生的正常事件。有 的也称为开关事件。
■ External event - An event which is normally expected to occur
■事件符号原则上有上述四种,其中只有 gp矩形符号是必须往下分析的事件,其余 *三种都是无须进一步分析的事件,故将
此三者合称为基本事件或底事件。
*在事件符号内必须填写事件。从分析事故 的目的出发,“事件”就是构成事故的 因素。所填入的事件必须是具体事件, 不得笼统、含糊不清。
■逻辑门符号是表示相应事件的连接特性 符号,用它可以明确表示该事件与其直 接原因事件的逻辑连接关系。
■ The logic gates are the fault tree graphic operators.
■①与门:可以连接数个输入事件Ei、
I E2.……、En和一个输出事件E,表示 生——仅当所有输入事件都发生时,输出事件
E才发生的逻辑关系。
•AND indicates that all the faults feeding into the AND gate must occur for the output fault to occur.

■②或门:可以连接数个输入事件Ei、
、 E2......En和一个输出事件E,表示至少一
-9—个输入事件发生时,输出事件就发生。
■An OR gate is the opposite of an AND. Any of the input events occurring would result in the event fault.
Ei
e2
En

■ The more AND gates you use, the safer the system is, AND gates denote a fault tolerance; for example, for a braking subsystem failure both the primary brake AND the backup eddy-current brake must fail.
③非门:表示输出事件 是输入事件的对立事 件。

31
④特殊门
、.A.表决门:表示仅当输入事件有m个 W (m<n)或m个以上事件同时发生时,输
出事件才发生。符号是如下。显然,或 门和与门都是表决门的特例。或门是 m=l时的表决门;与门是M=N时的表决 门。
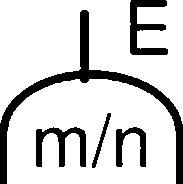
Ei E2
En
B.异或门:表示仅当单个输入事件发生 时,输出事件才发生。
不同时发生
Ei
e2
En
C.禁门:表示仅当条件事件发生时,输 入事件的发生方导致输出事件的发生。
Ei
D.条件与门:表示输入事件不仅同时发生,而 且还必须满足条件A,才会有输出事件的发生。
E
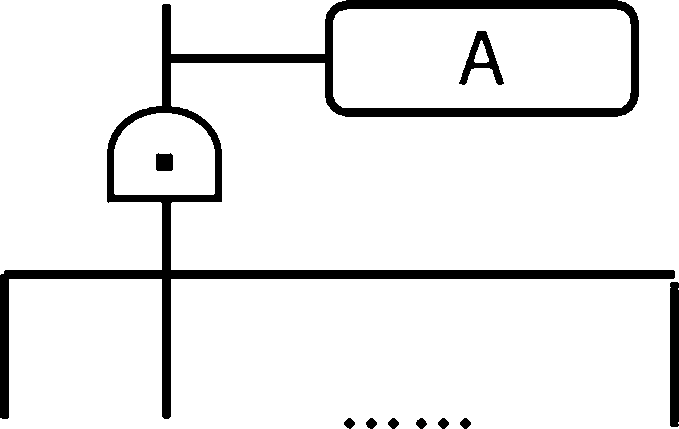
Ei E2 En
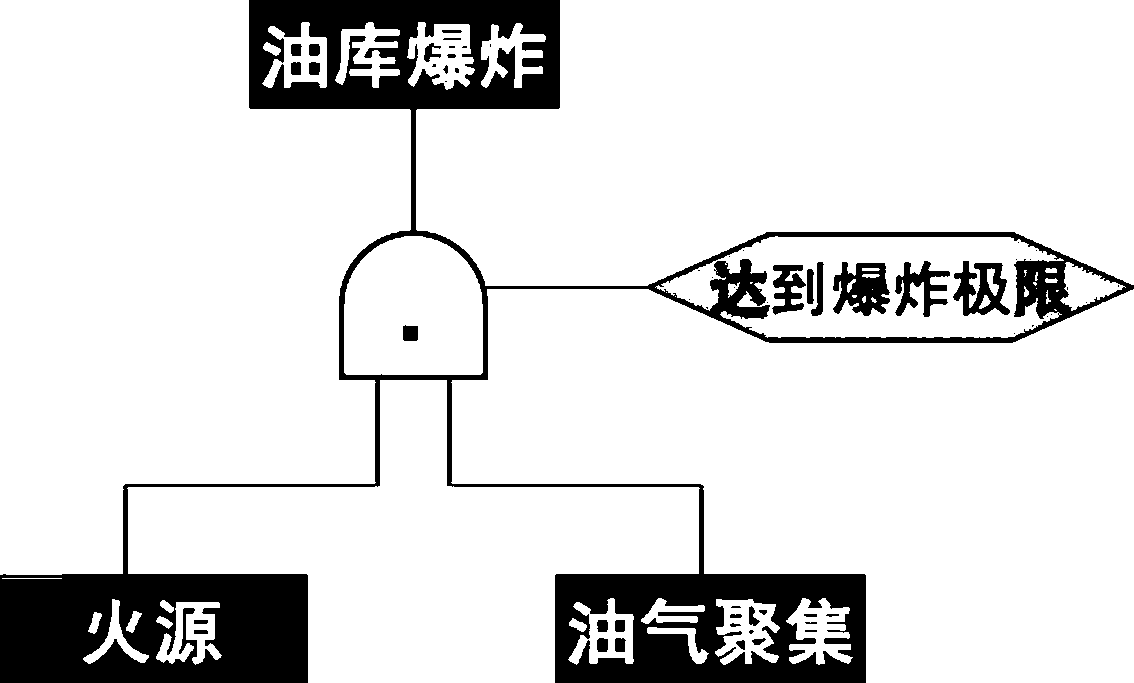
E.条件或门:表示输入事件至少有一个发生, 在满足条件A的情况下,输出事件才发生。
I— A ffi

Ei E2
En
3)转移符号
转移符号表示部分事故树图的转入和转
出。当事故树规模很大或整个事故树中
多处包含有相同的部分树图时,为了简
化整个树图,便可用转入和转出符号。
转入

转出
■事故树编制是事故树分析中最基本、最关键的
=1
环节。
■编制工作一般由系统设计人员、操作人员、和 可靠性分析人员组成的编制小组来完成,经过 反复研究,不断深入,才能趋于完善。
■通过编制过程能使小组人员深入了解系统,发
现系统中的薄弱环节,这是编制事故树的首要
目的。
■事故树的编制是否完善直接影响到定 性分析和定量分析的结果的正确性, 关系到事故树分析的成败,所以事故 树编制这一环节是非常重要的。
■编制方法一般分人工编制、计算机辅 助编制两类。
—、人工编制
1.编制事故树的规则
■事故树的编制过程是一个严密的逻辑 推理过程,应遵循以下原则:
①确定顶上事件应优先考虑风险大的事 故事件。能否正确选择顶上事件,直 接关系到分析结果,是事故树分析的 关键。应当把容易发生且后果严重的 事件优先做为分析对象,即顶上事件; 也可以把发生频率不高但后果严重以 及后果不太严重但非常频繁的事故做 为顶上事件。
②合理确定边界条件。在确定了顶上事件后,为 了不致使事故树过于繁琐、庞大,应规定被分 » 析系统与其他系统的界面,并作一些必要的合 理的假设。
③保持门的完整性,不允许门和门直接相连。事 故树编制时应逐级进行,不允许跳跃;任何一 个逻辑门的输出都必须有一个结果事件,不允 许不经过结果事件而将门与门直接相连,否则, 将很难保证逻辑关系的准确性。
④确切描述顶事件。明确地给出顶事件的定义, 即确切地描述事故的状态,什么时候在何种条 件下发生。
⑤编制过程中及编成后,需及时进行合理的简化。
2.编制事故树的方法。
aɪ
人工编制事故树的常用方法为演绎法,它是通 过人的思考分析顶事件是怎样发生的。
① 首先确定系统的顶上事件,找出直接导致顶上 事件发生的各种可能因素或因素的组合即中间 事件。
② 在顶上事件与其紧连的中间事件之间,根据其 逻辑关系画上逻辑门。
③ 然后再对中间事件进行类似的分析,找出直接 原因,逐级向下演绎,直到不能分析的基本事 律为止。
④ 这样就得到用基本事件符号表示的事故树。
二、编制举例
I例:用演绎法编制“油库静电火灾爆炸”事故树。 *■油库所储存的油品是汽油、煤油、柴油、原油、 * 松节油等,这些油品具有燃烧爆炸的危险性, 一旦发生燃烧爆炸事故,将会造成人员伤亡, 财产损失,甚至危急周围人群的安全。
rɪ
■油库静电火灾爆炸是危害性极大的事故,因而 可以将“油库静电火灾爆炸”事故作为事故树 的顶事件并编制其事故树。
■编制事故树从顶事件开始,逐级分析导致顶事 件发生的中间事件和基本事件,按逻辑关系, 用逻辑门符号连接上下层事件。例如:“油气 达到可燃浓度”与存在“火源”两个中间事件 同时存在并且达到爆炸时,顶事件才能发生。
■作业4: “以钢瓶内液化气泄漏燃爆”
为顶上事件编制事故树(假设钢瓶 是放在屋内)。

第三节事故树的定性分析
■事故树定性分析就是对事故树中各事件不考虑
发生概率多少,只考虑发生和不发生两种情况。
通过定性分析可以知道哪一个或哪几个基本事
■X
件发生,顶上事件就一定发生,哪一个事件发 生对顶上事件影响大,哪一个影响少,从而可 以釆取经济有效的措施,防止事故发生。
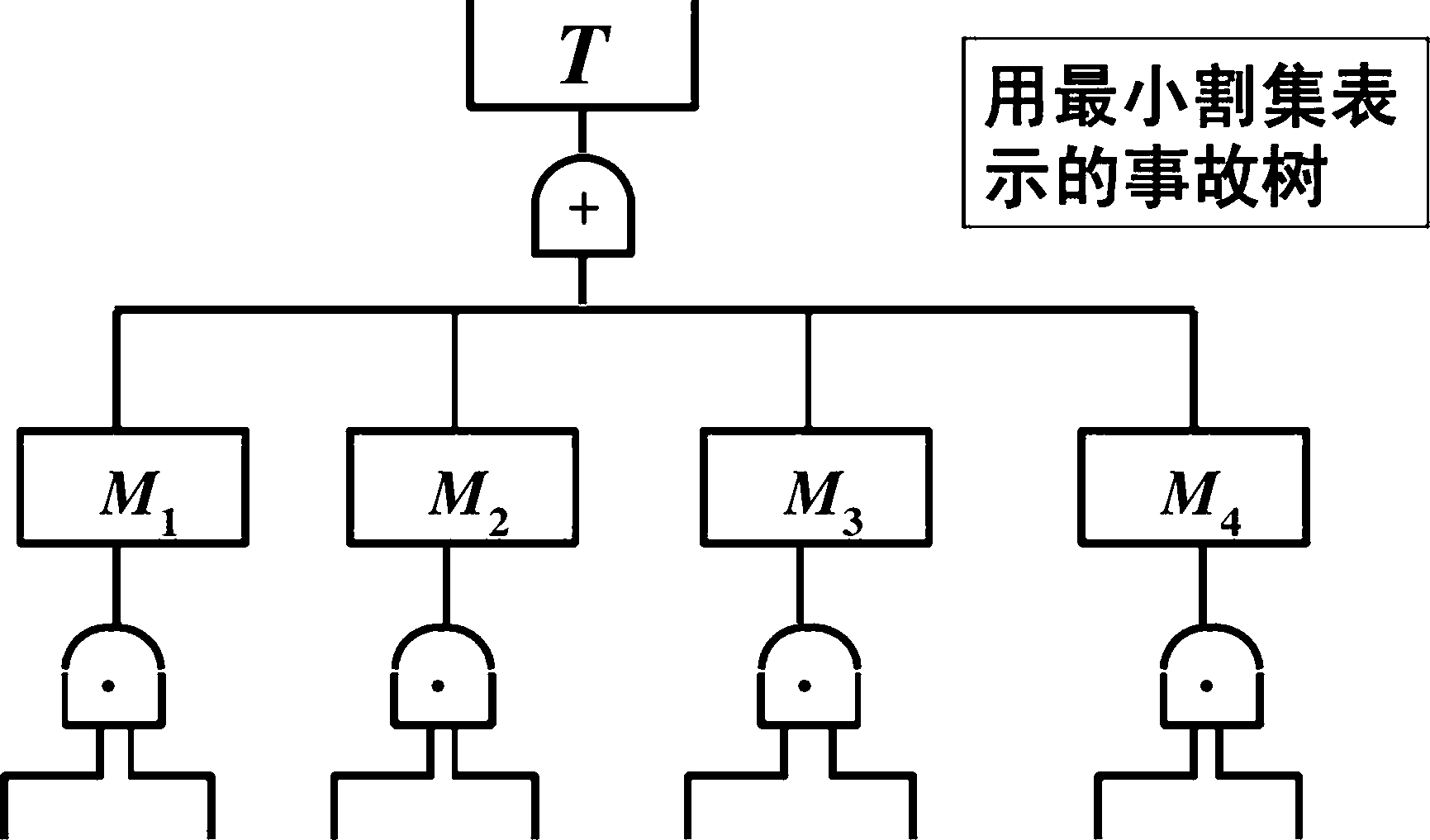
■事故树定性分析,就是根据事故树求取其最小 割集和最小径集,计算各基本事件的结构重要 度,在此基础上确定安全防灾对策。
M.
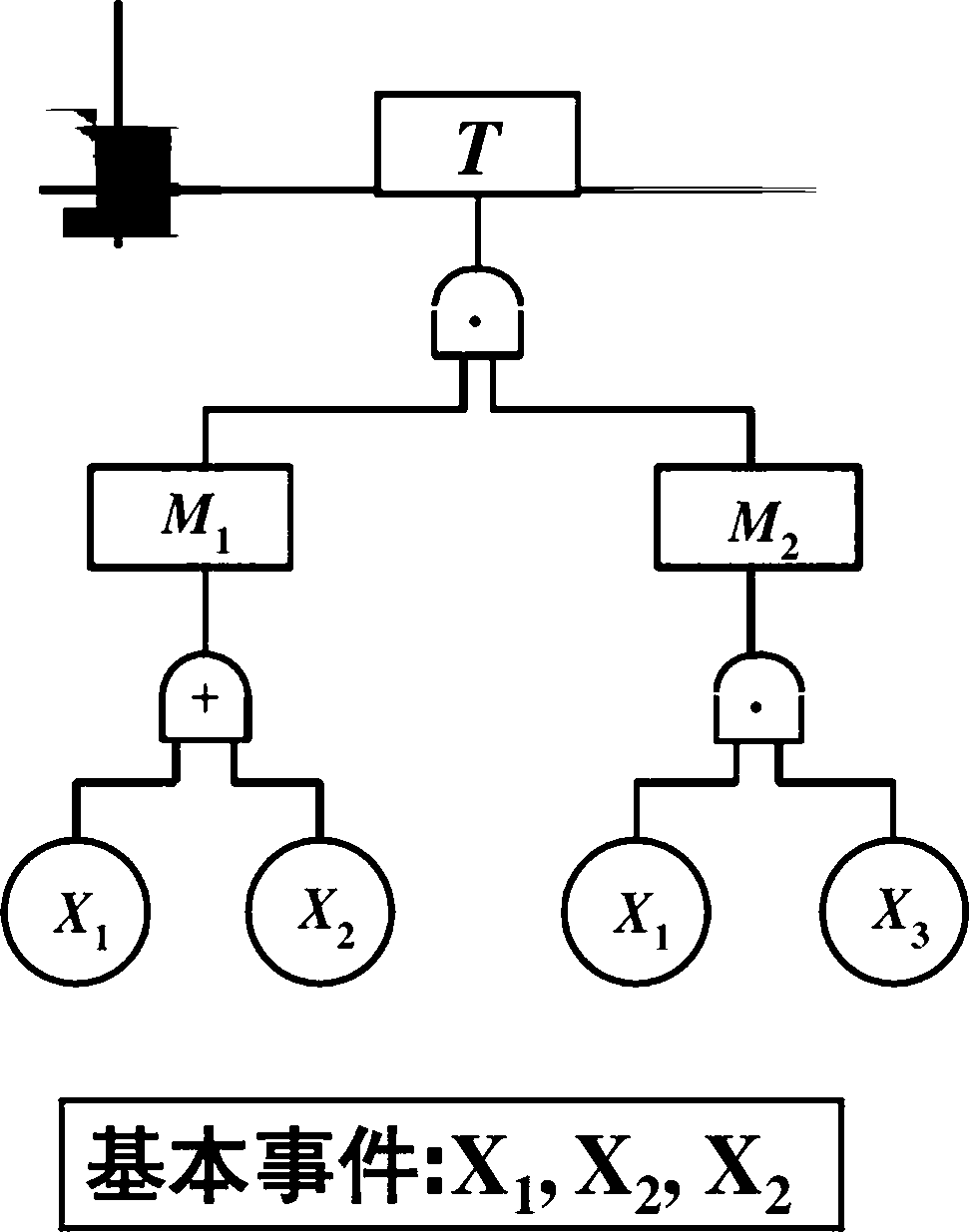
基本事件:X1,X2, x2
X3
|
ɪɪ |
T | ||
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
] |
0 |
|
1 |
1 |
] |
1 |
|
0 |
1 |
1 |
0 |
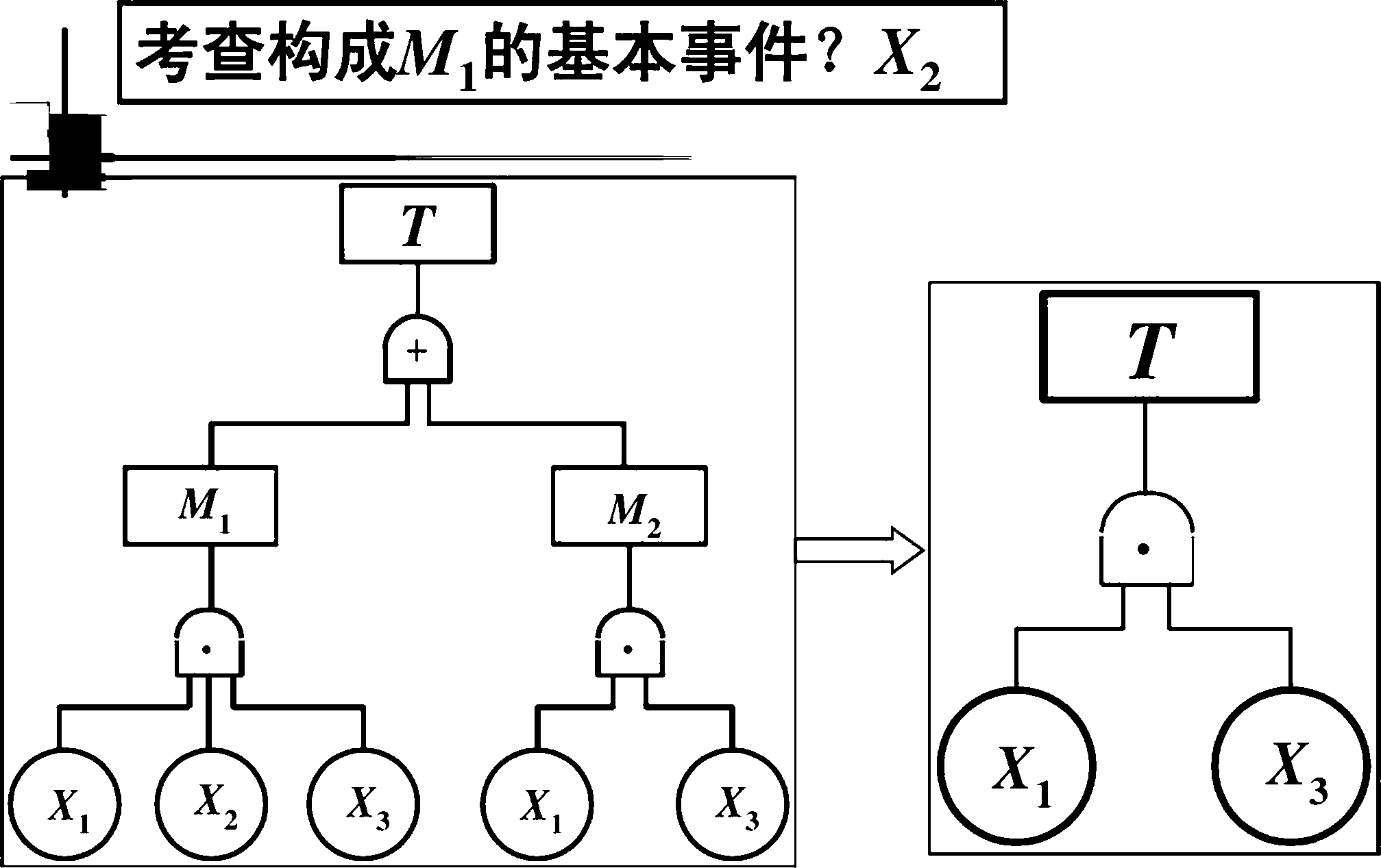
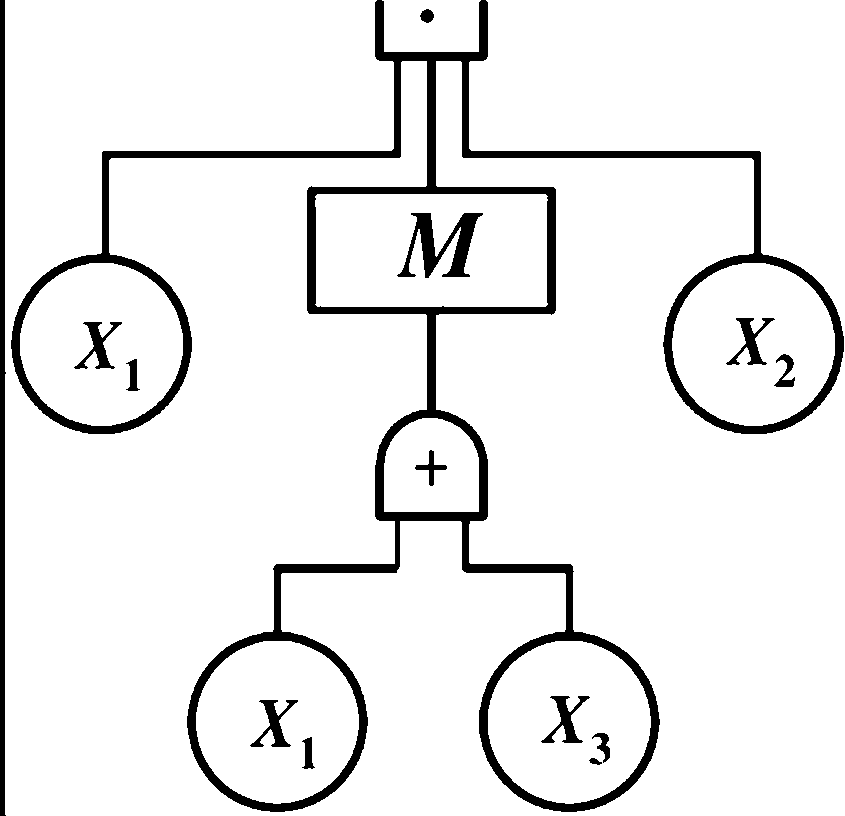
化简下列事故树
rɪi
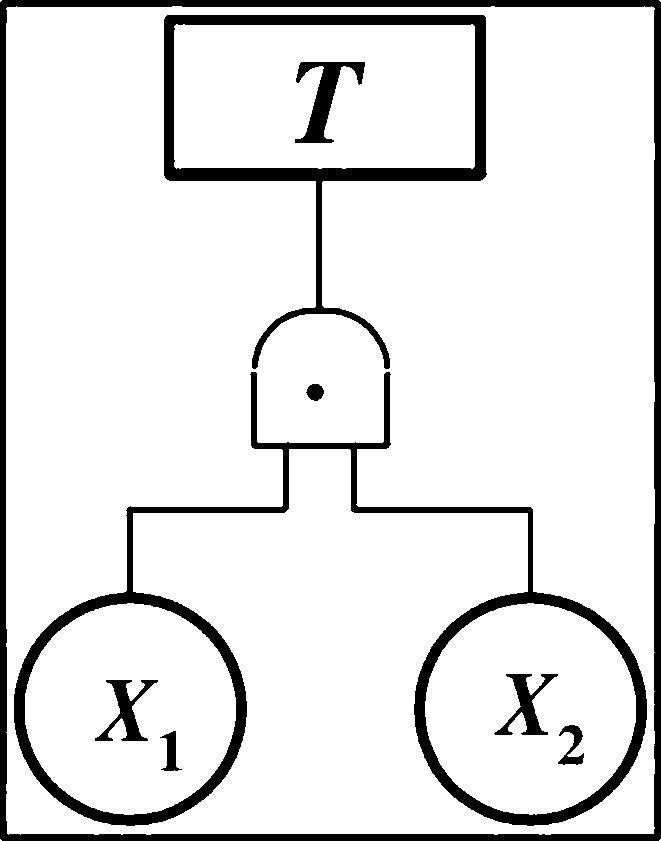
48
■ 1、逻辑值和逻辑变量
■逻辑值: 状态。
“(T和“1”,表示两种相反的
■逻辑变量:在某一过程中可取不同数值 的量称为变量,只能取“0”和“1”两个 值的变量,称为逻辑变量。
■1+1= 1
■逻辑或(逻辑加)"+”或 逻辑表达式为:Z=A+B (AUB)
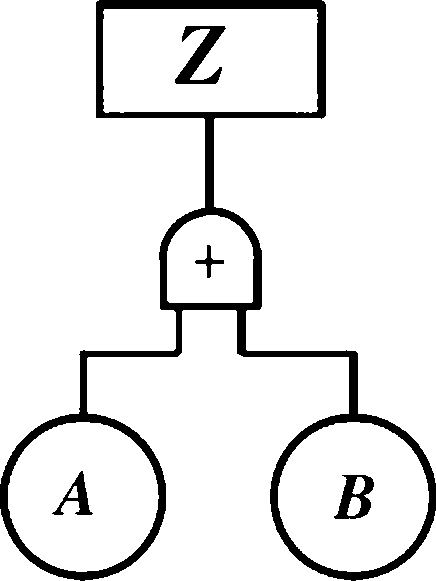
|
0+0=0 0+1 = 1 1+0 = 1 1+1=1 |
4+1=1 4+0=4 |
如果有〃个逻 辑变量,则 | |||
|
n | |||||
|
z = a + +ʌɜ+......+An | |||||
逻辑与(逻辑乘)“X”或“rr
士 ——
逻辑表达式为:Z=A B (ADB)
|
0-0=0 0-1=0 1-0=0 1-1=1 | |
A-0=0
A-1=A
z
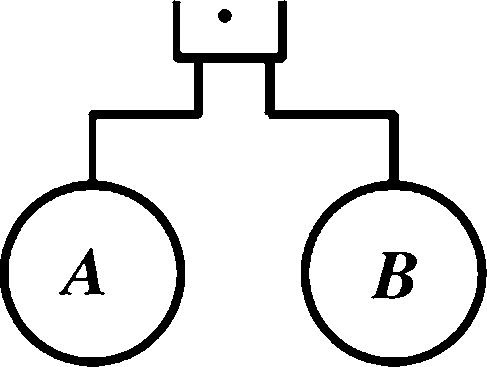
如果有〃个逻 辑变量,则
Z = Al-A2-A3.....An
有两条运 算法则
逻辑或 交换率:A+B=B+A
结合率:A+(B+C)=(A+B)+C
同―率:4+0=4
0—1率:A + l = l
等寫率:A+A=A
逻辑加 交换率:A'B—B'A
结合率:A- (B・C)=0・B) C
同―率:A-1=A
0—1率:4.0=0
等寫率:A-A=A
■逻辑或和逻辑与还有如下性质 ■乘对加的分配率:A (B+C) =AB+AC ■加对乘的分配率:A +BC =(A+B )(A+C)
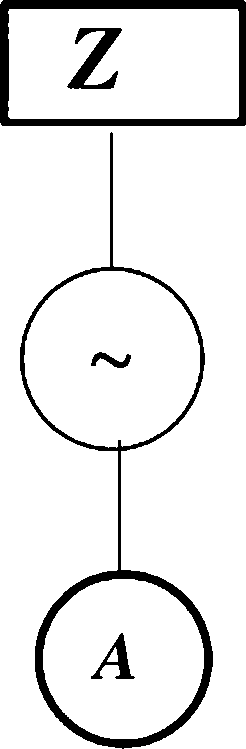
■逻辑非有如下基本性质:
A +A = 1
AA = Q
双重否定率
A = A
■吸收率:A +AjB = A
. A (A+B)=A
■摩根定律
和的非等于非的积:a + b = a b
积的非等于非的和:
aJb = a+b
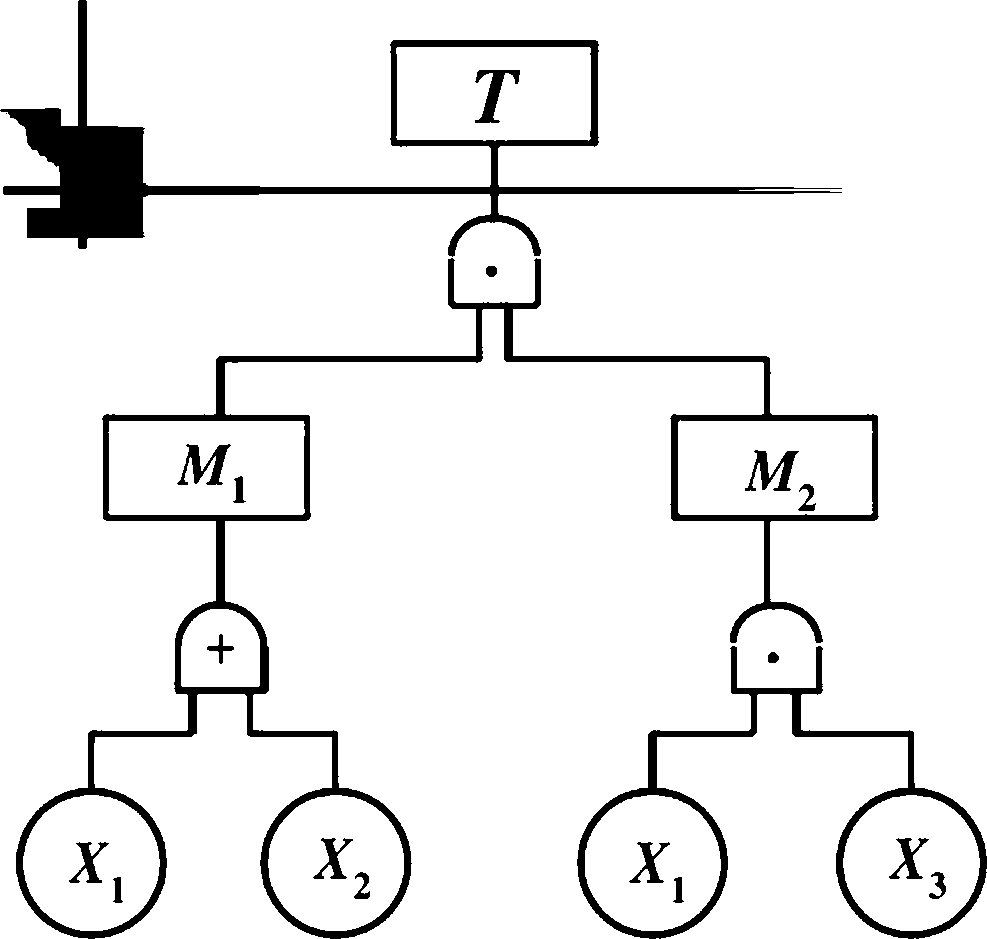
= (X| + X2)X/3
= X|X|Xa + X,X|Xa ɪ ɪ —ɪ —
= X|X3 + X,X』3 1- ɪ
= X|XJ1+X,) L 。 J
=5
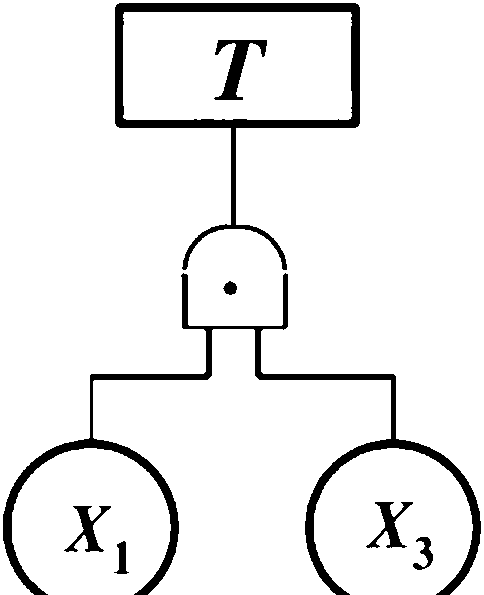
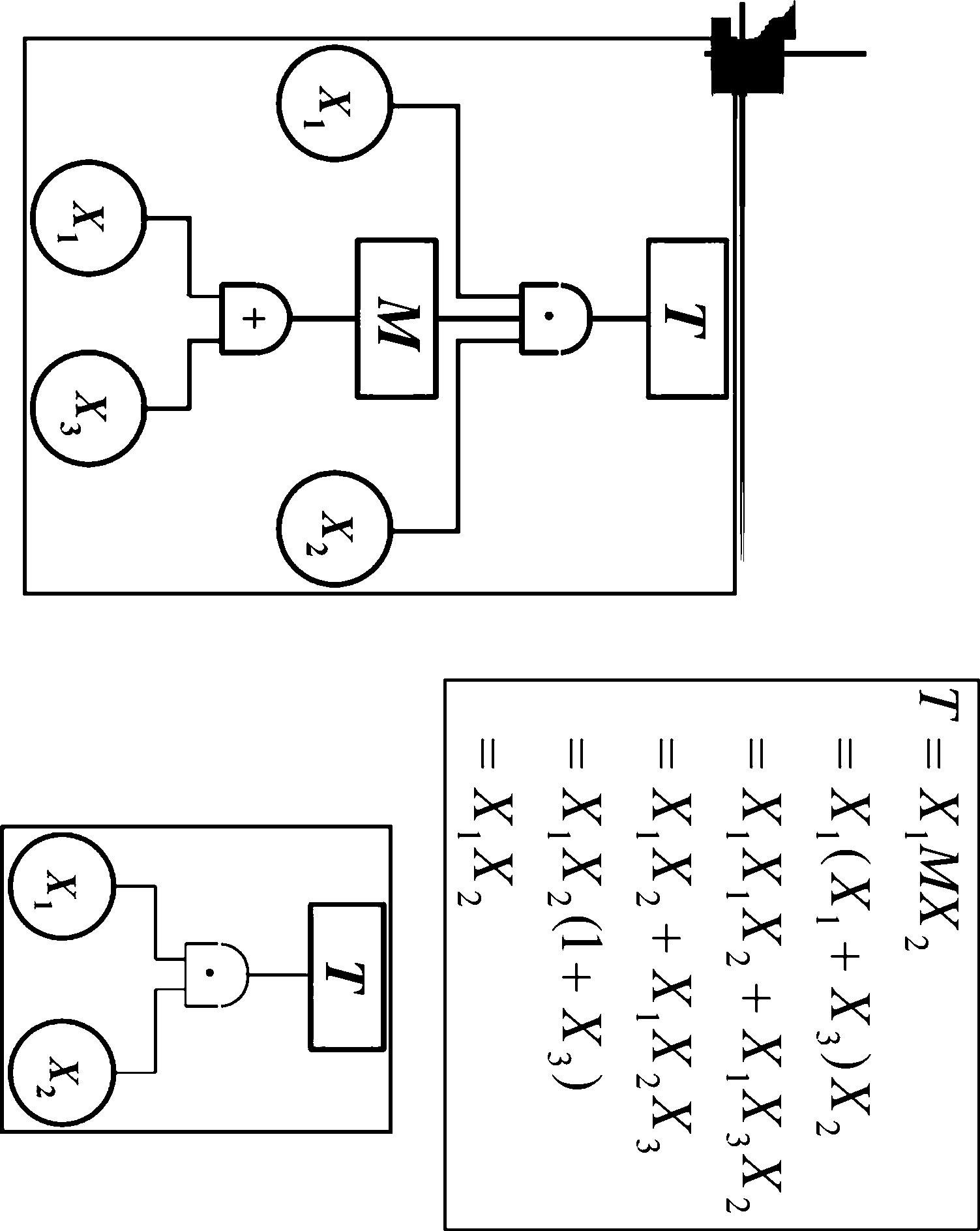
a
化简事故树
T

I ~I
KZT 巨
'x*x + 'x・Zx + 'x」x + *x*x 二
'X •,X + ^-^+^-^ + ^-^(^ + 1) = 'XAX+'X'ZX + 'X^X + "X'£XCX + 1) + "XAXJX = E 'x3x+'x・'x + 'x」x+
*xMx + *xMx・‘X + *x3x・* 二
'X3X+'X・'X + ‘X」X+
rɪʒi (汶 + *X •以心 ++ lX)=
L!I Cx + "x'£x)[£x + Cx + *)]=
原枷Z—£图924 (' X + *" X +勺)='由二丄
|
ɪ | |||
|
M. M. Mr Ma ɪ ɔ q | |||
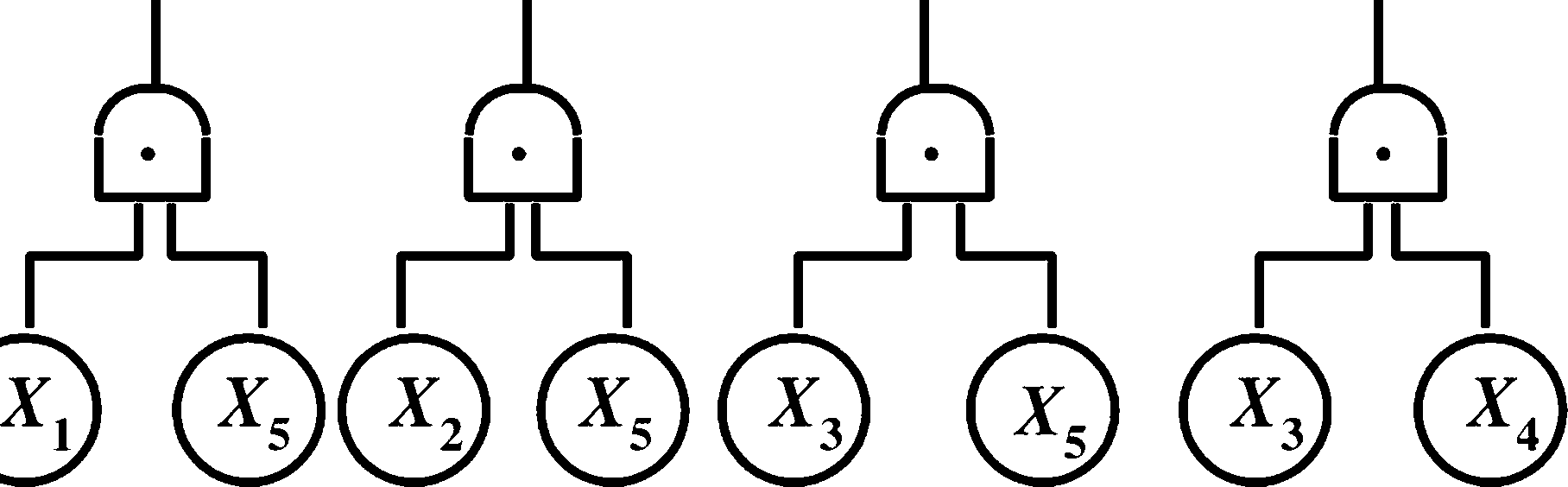
二、最小割集和最小径集
割集和最小割集(P45)
W①在事故树中,如果所有的基本事件都发 生则顶上事件必然发生。
② 在很多情况下并非如此,往往是只要某 个或几个基本事件发生顶上事件就能发 生。
③ 凡是能导致顶上事件发生的基本事件的 集合就叫割集。
④ 割集就是系统发生故障的模式。 侦
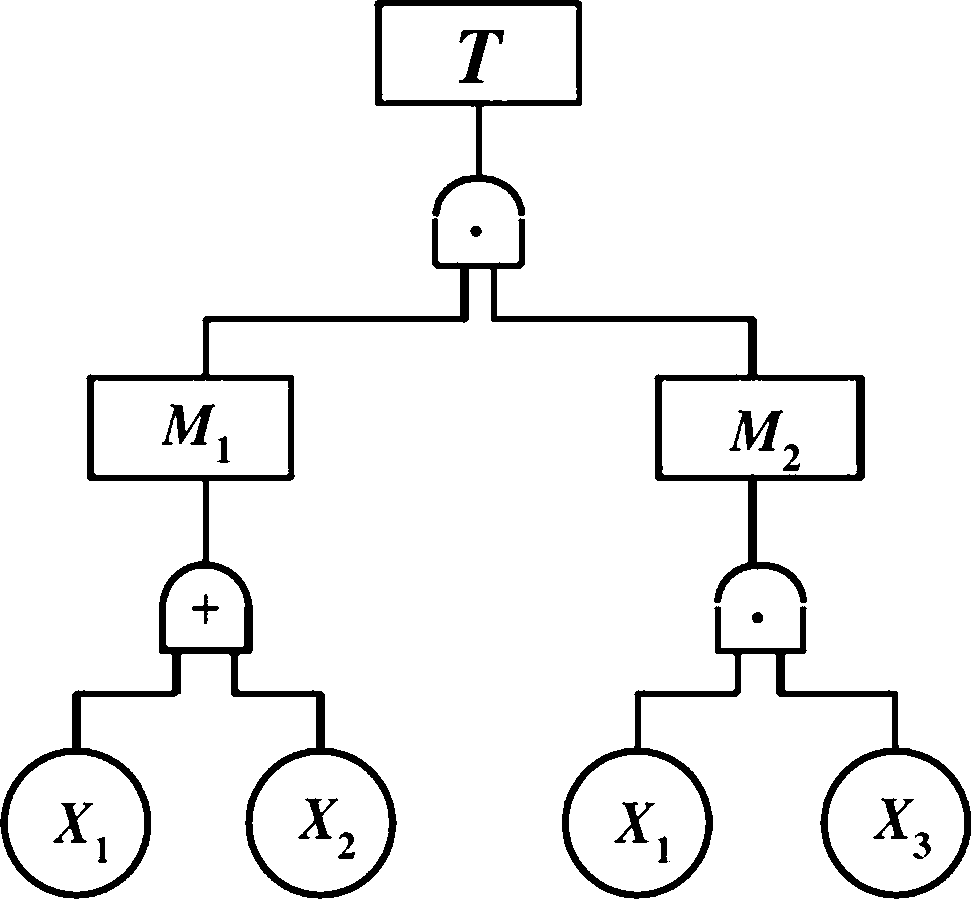
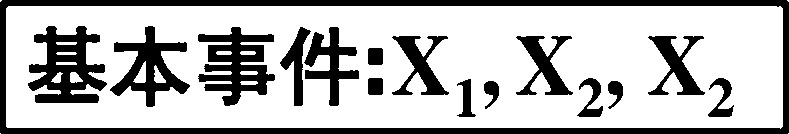
|
ɪɪ |
X3 |
T | |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
] |
0 |
|
1 |
1 |
] | |
|
0 |
1 |
1 |
0 |
⑤ 在一棵事故树中,割集数目可能有很多,而在 内容上可能有相互包含和重复的情况,甚至有
El rɪ
II
* 多余的事件出现,必须把他们除去,除去这些 ■ 事件的割集叫最小割集。也就是说,凡能导致 顶上事件发生的最低限度的基本事件的集合称 为最小割集。
⑥ 在最小割集里,任意去掉一个基本事件就不成 其为割集。
⑦ 在事故树中,有一个最小割集,顶上事件发生 的可能性就有一种。事故树中最小割集越多, 顶上事件发生的可能性就越多,系统就越危险。
2、集合
■集合:就是满足某种条件或具有某种属 性的事物的全体。
■集合的每一个成员称为这个集合的元素。
■一个割集所包含的几个基本事件就组成 一个集合,这个集合中每个基本事件就 是它的元素。一个割集含有X]、X2两个 基本事件,则记为{X], X2} o
II
■所谓并集就是把两个集合A和B的元素合 并在一起。如果合并的元素构成的集合 叫S,那么S=A+Bo事故树中或门的歸出 事件就是所有输入事件的并集。
■若两个集合A与B有公共元素,则公共元 素构成的集合P称为A与B的交集,记为 P=A Bo事故树中,与门的输出事件就 是输入事件的交集。
3、最小割集的求法
最小割集的求法有很多,主要布尔代数法 和行列式法。
1.最小割集求法
①布尔代数化简法。
对比较简单的事故树可用此法求取。
②布尔代数法求最小割集的步骤是:
■首先列出事故树的布尔表达式,即从事故 树的第一层输入事件开始,“或门”的输 入事件用逻辑“加”表示,“与门”的输
入事件用逻辑“积”表示。再用第二层输
入事件代替第一层,第三层输入事件代替
第二层,直至事故树全体基本事件都代完
为止。布尔表达式整理后得到若干个交集, 每一个交集就是一个割集,然后再利用布 尔代数运算定律化简,就可以求出最小割 集。
寸X.IX+SX.ZX.IX+SX.SXH 寸X.IX+寸WX.SX+SX.SX.IX+ sx.sx+sx.mx+sx.sxkxh ■ 寸X.IX+寸X.SX.SX+SX.SX.IX .SX.SX+SXKX.IX+Sx3x.sx.sxn ■ CX+SX.SX+SXXX).(IX+SX.SXII■ FX+SX.CX+ZXH.CX+SXWXII■ cx+sx 顶).(Ix+sxwxll■. CX+§(IX+或iiedhz ■
画“享>@
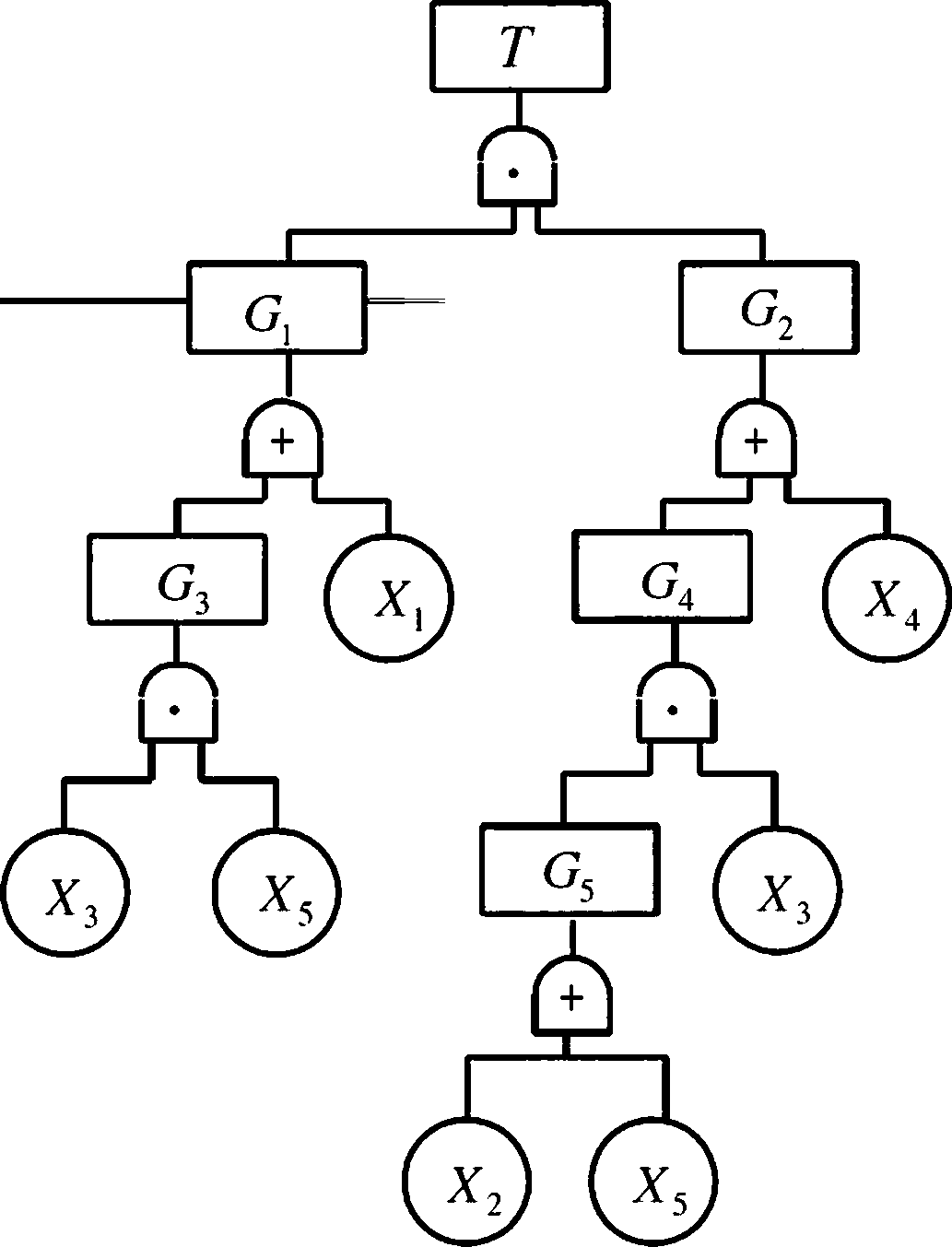
③举例P77图3-21
7 =砧2=(归3+印(乂]+乂2)
= (X« + X5・&)(X] + X2)
=[X] • (X3 + X4) + X5 • (X2 + 乂6 + X7)](X] + X2)
二(X1X3 + X/4 + X5X2 + X5X6 + X5X7 )(X] + X2)
fXX +X|X8 +X1X4X1 +X1X4X2 +X5X2X1
丄 J 1 1 J J ɪ I ɪ ɪ I 匕 J J ɪ
+X,XsX, +X5X6X1 +XSX6X9 +X5X7X1 +X5X7X2
X5X6X2 +X5X7XI+X5X7X2
=X1X3 +X1X4 +X』5 +X』6X| +X5X7X1
© ©
④行列法
■行列法是1972年由富赛尔提出的,所以又称富 赛尔法。这种方法的原理是:与门使割集的大 小庄增加,或门使割集的数量增加。
■从顶上事件开始,按逻辑门顺序用下面的输入 事件代替上面的输出事件,逐层代替,直到所 着墓本事件代完另止。
■在代替过程中,“或门”连接的输入事件纵向 列出,“与门”连接的输入事件横向列出。这 样会得到若干基本事件的交集,再用布尔代数 化简,就得到最小割集。
.举例(P44)
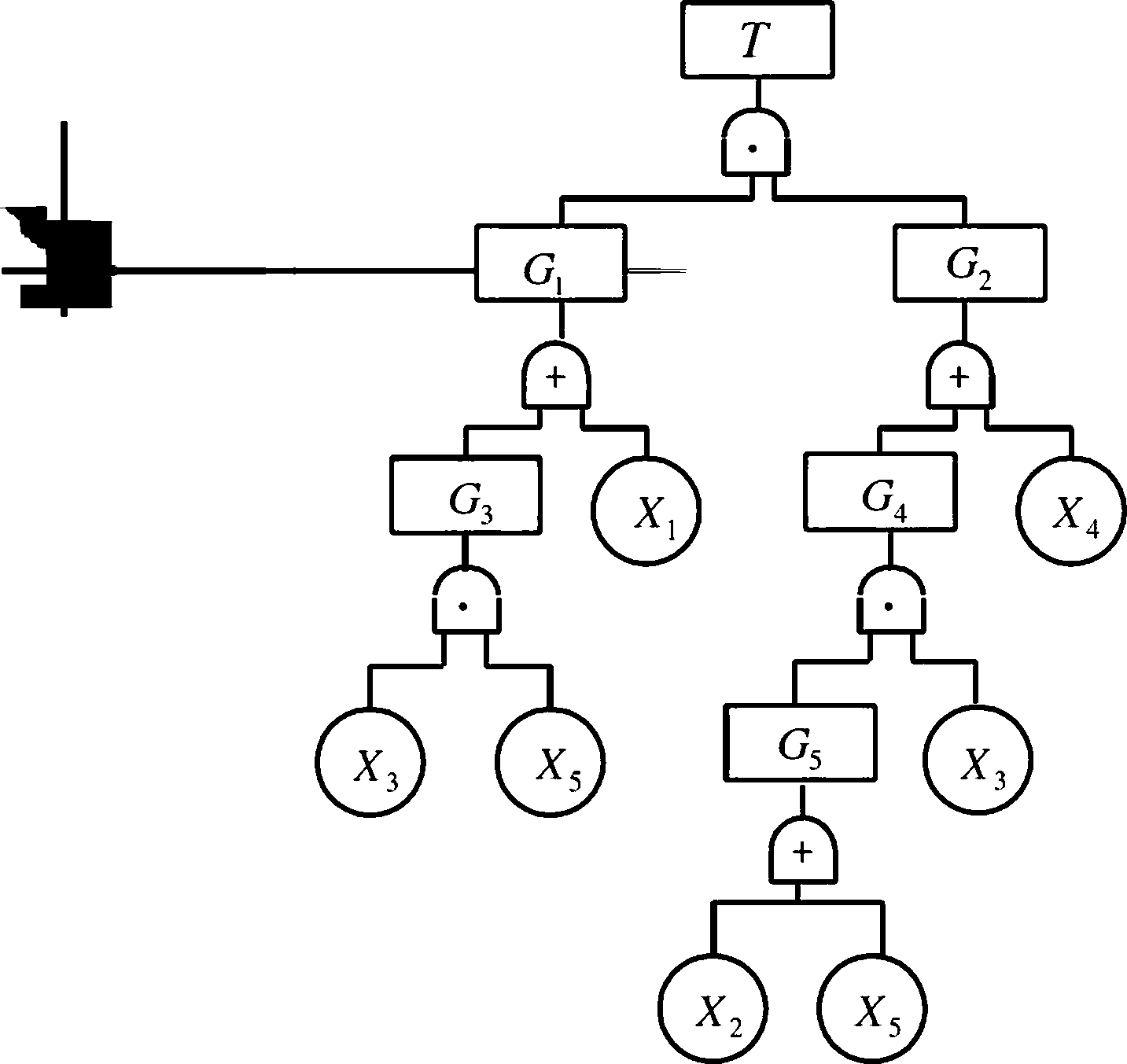

xq.x’ XE X3X5G5X3 x? • X5 • X4 、
4.径集与最小径集
①在事故树中,当所有的基本事件都不发
EI 4
生时,顶上事件肯定不会发生。
② 然而顶上事件不发生常常并不要求所有 基本事件都不发生,而只要某些基本事 件不发生顶上事件就不会发生。
③ 这些不导致顶上事件发生的基本事件的 集合称为径集。
④ 径集是表示系统不发生故障而正常运行
南穫会。 I、I
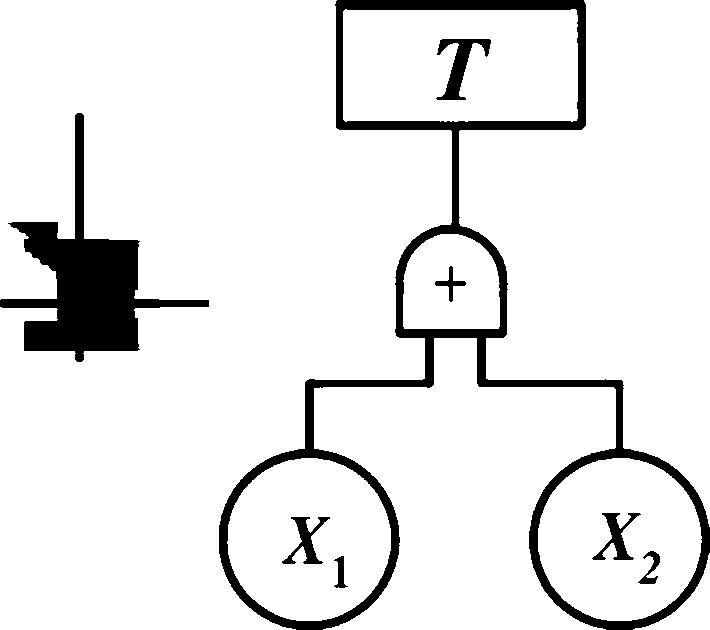
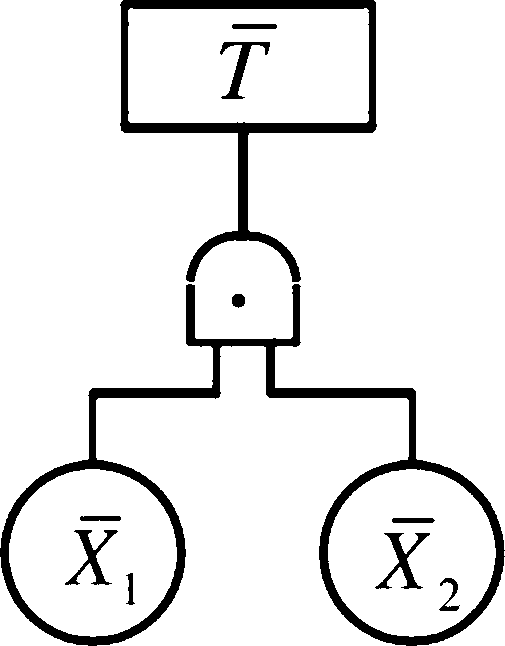
T


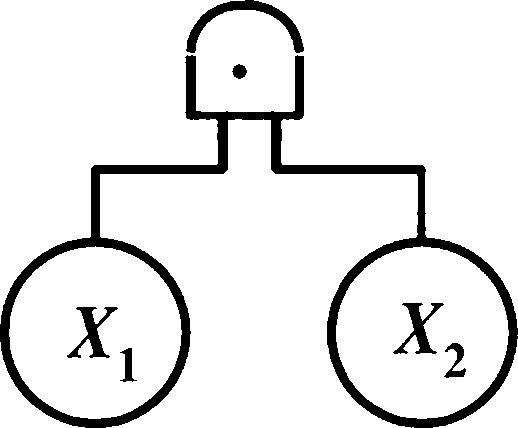
2
JL
⑤ 同样在径集中也存在相互包含和重复事 件的情况,去掉这些事件的径集叫最小 径集。也就是说凡不能导致顶上事件发 生的最低限度的基本事件的集合称为最 小径集。
⑥ 在最小径集里,任意去掉一个基本事件 就不成其为径集。
⑦ 事故树有一个最小径集,顶上事件不发 生的可能性就有一种。最小径集越多, 顶上事件不发生的途径就越多,系统也 就越安全。
5.最小径集求法。
①最小径集的求法是利用最小径集与最小
割集的对偶性,首先画事故树的对偶树,
即成功树,求成功树的最小割集,就是 原事故树的最小径集。
②成功树的画法是将事故树的“与门"全
部换成“或门”,“或门”全部换成
“与门",并把全部事件发生变成不发
生,就是在所有事件上都加,使之
变成原事件补的形式。经过这样变换后 得到的树形就是原事故树的成功树 ―
I g
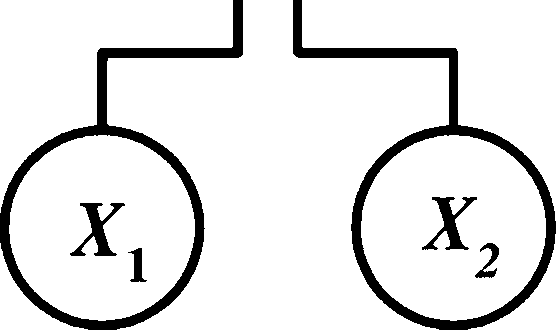
和的非等于非的积:
T = A+B
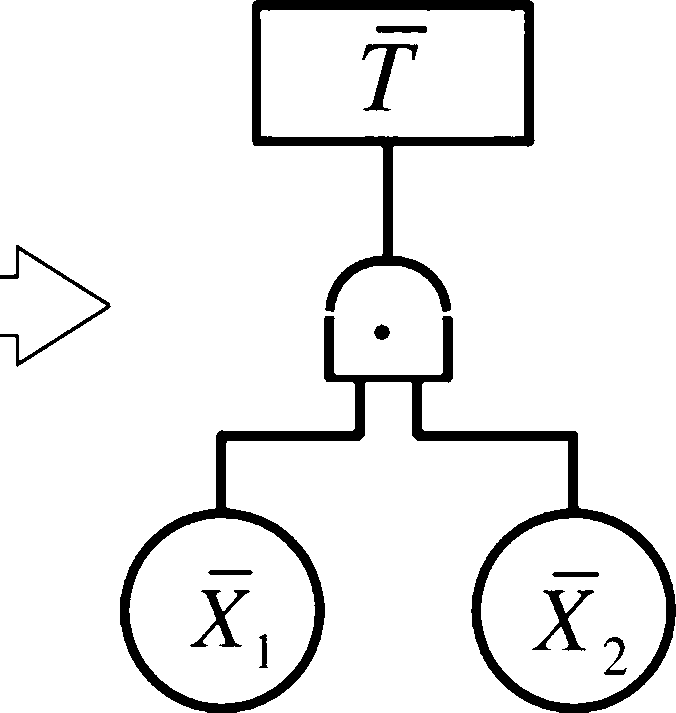
A+B=AB
^>T = AB
HE
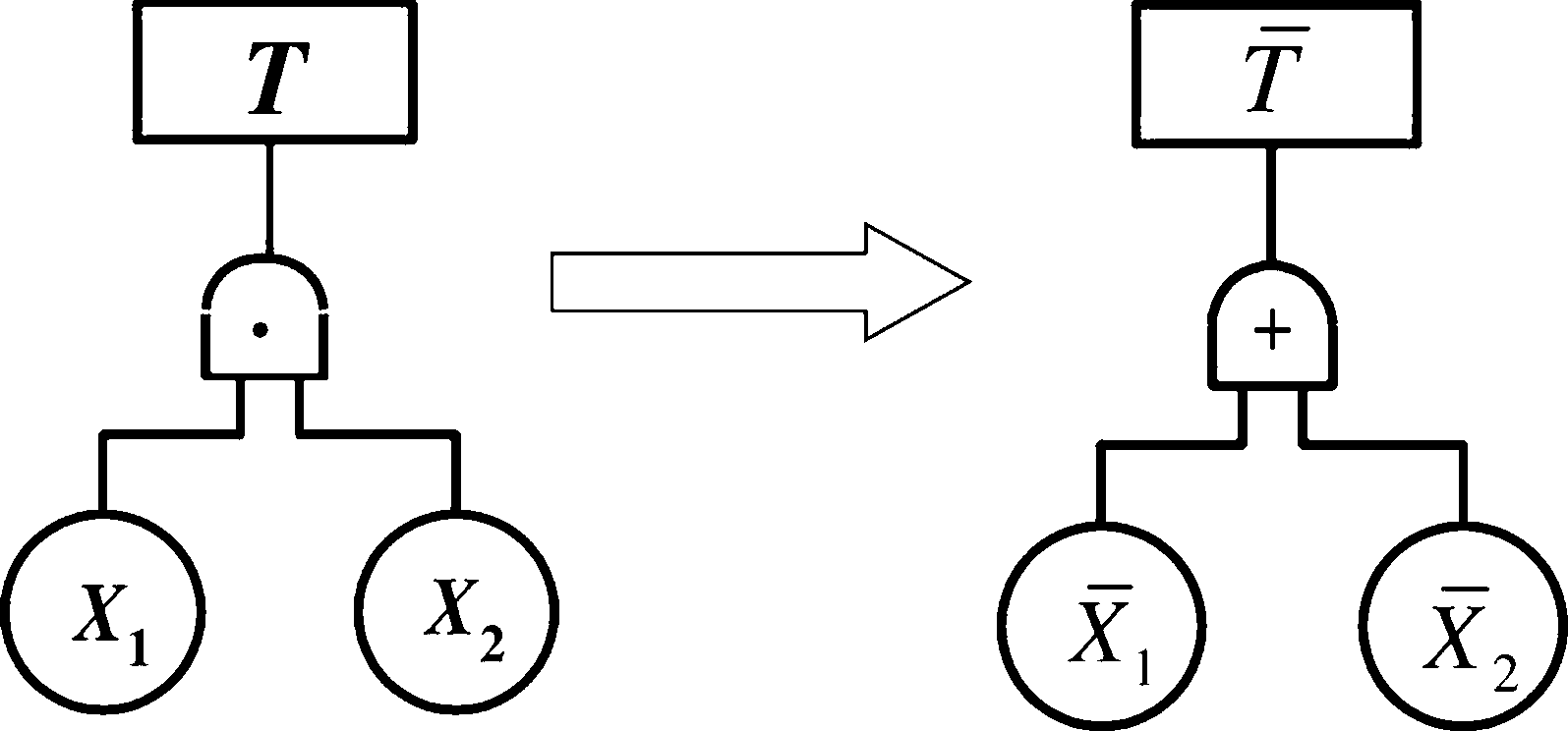
积的非等于非的和:A-B = A + B
t = ab^^t = a+b
③ 同理可知,画成功树时事故树的“与门" 要变成“或门",事件也都要变为原事 件非的形式。
④ 条件与门、条件或门、限制门的变换方 式同上,变龍M把条件作为基本事件处
II
理。
⑤ 举例:P52
⑥ 用最小径集表示的等效树也有两层逻辑 门,与用最小割集表示的等效树比较, 所不同的是两层逻辑门符号正好相反。
ɪl
5
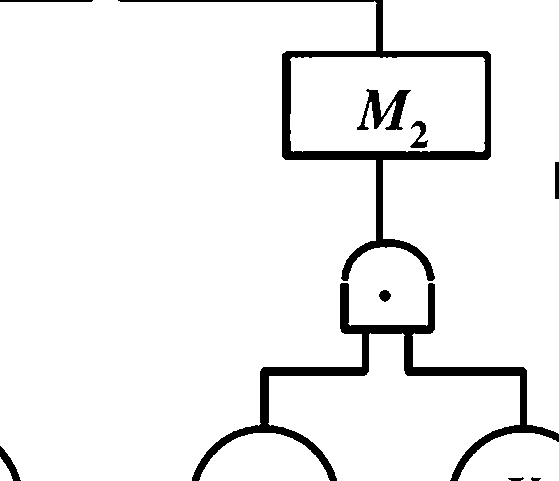
ɪl
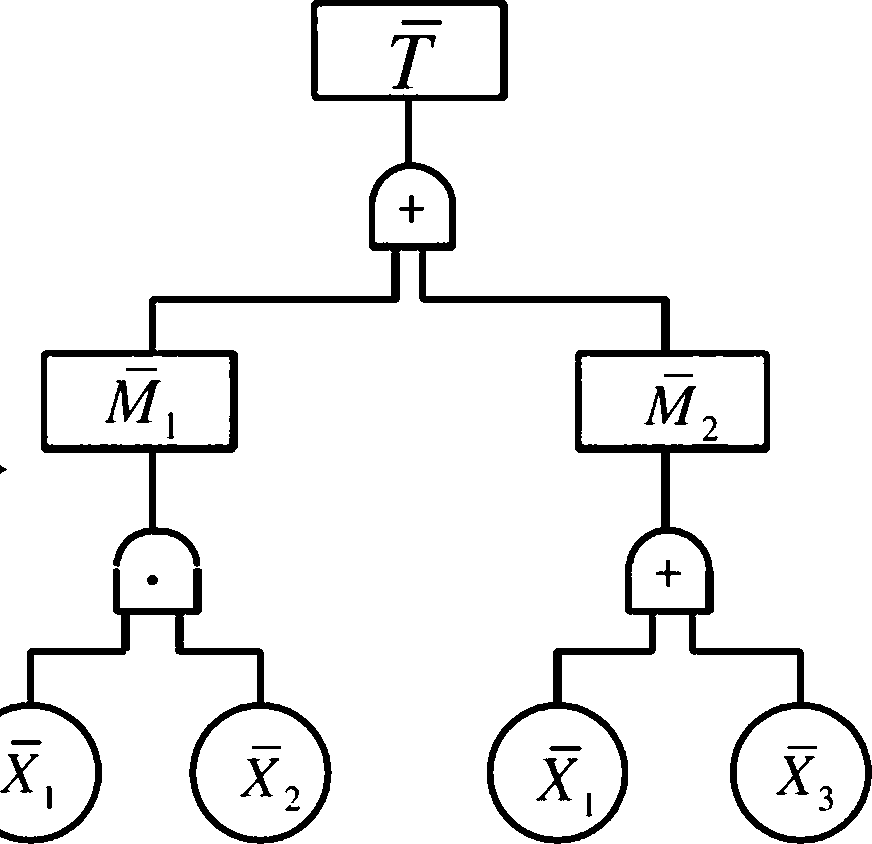
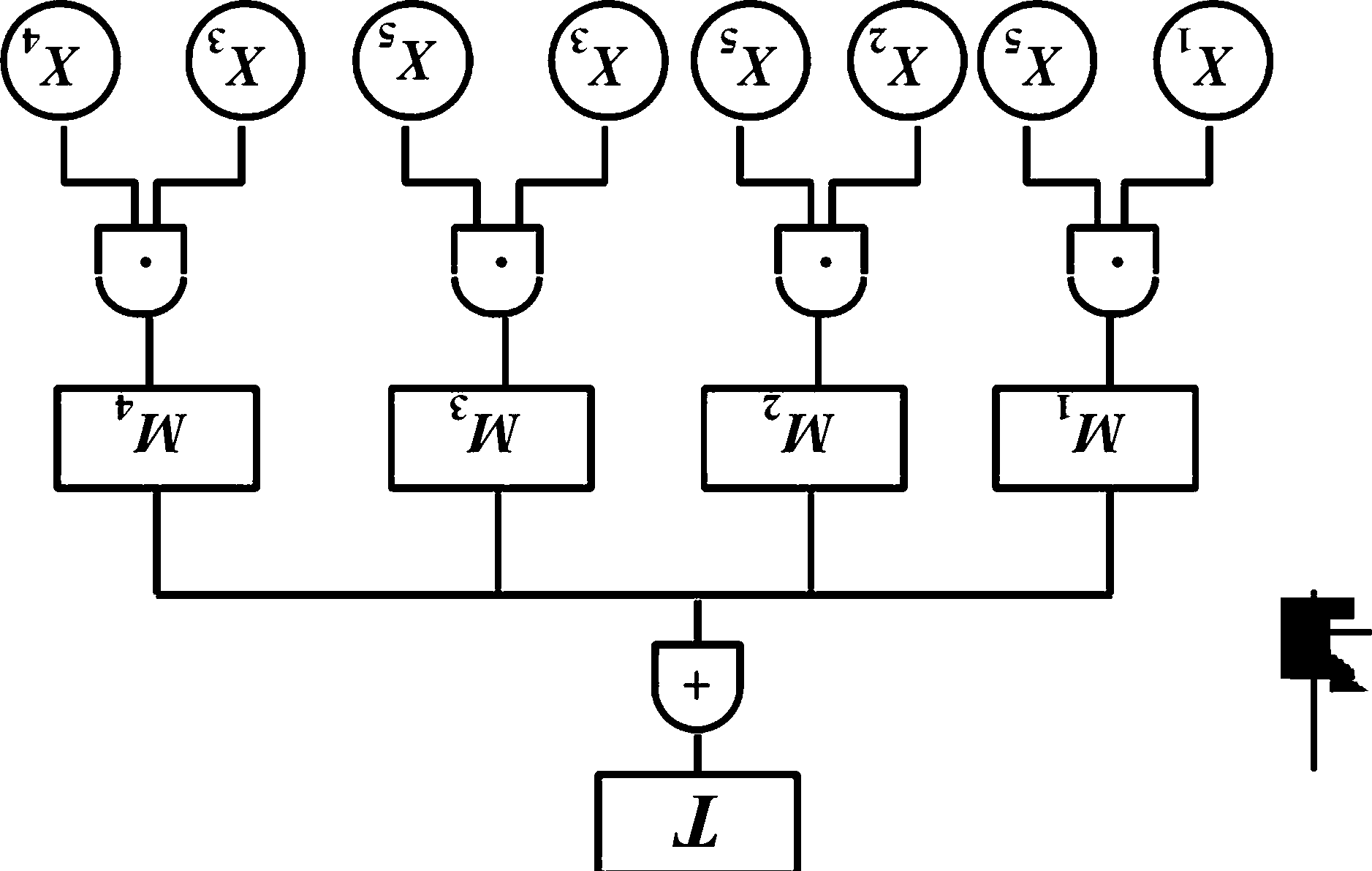
P76 图 3-20 化成功树
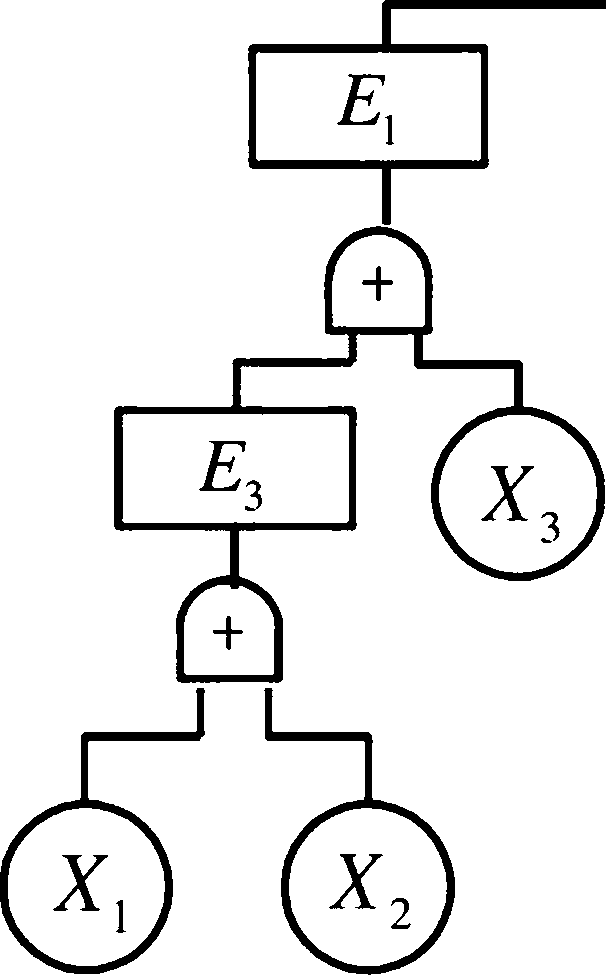
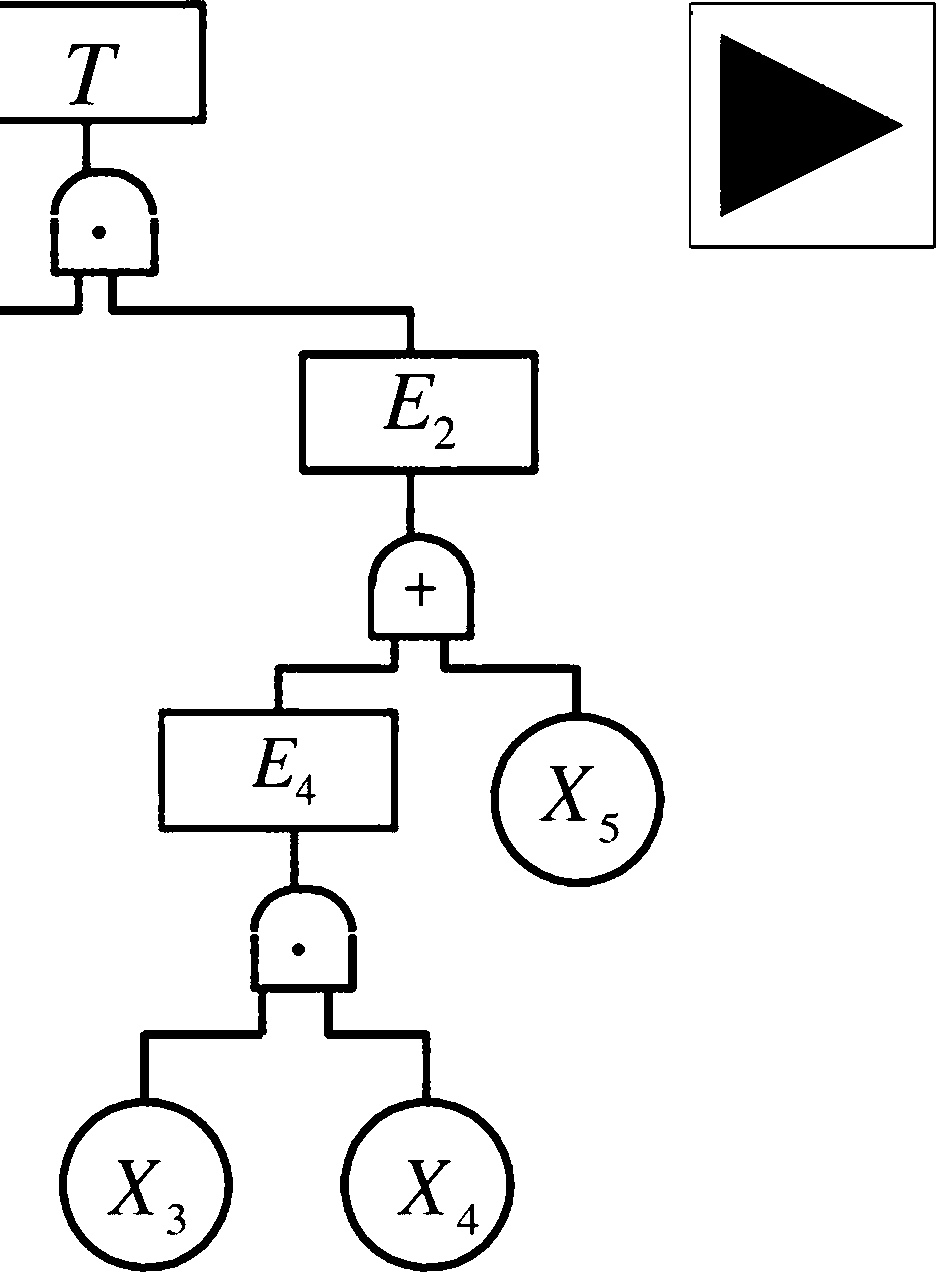
84
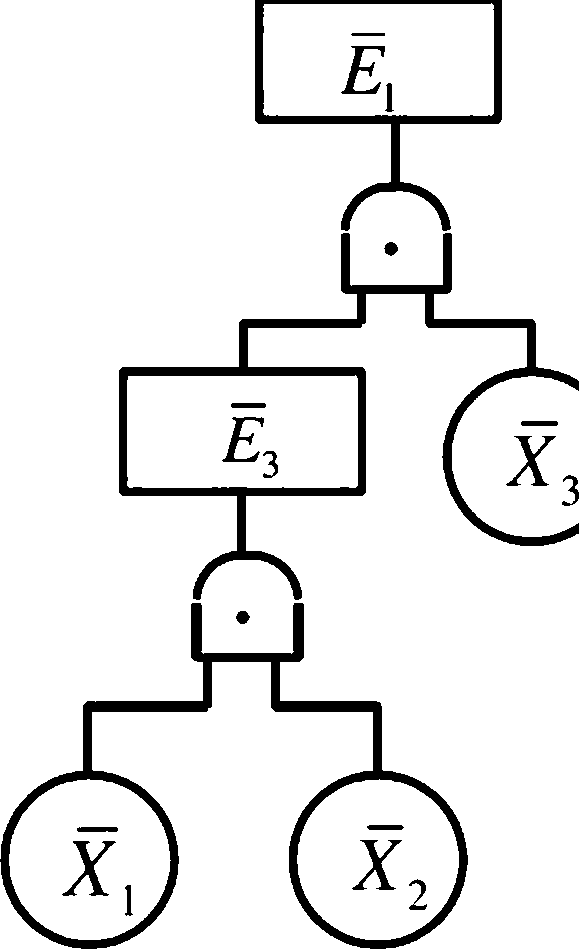
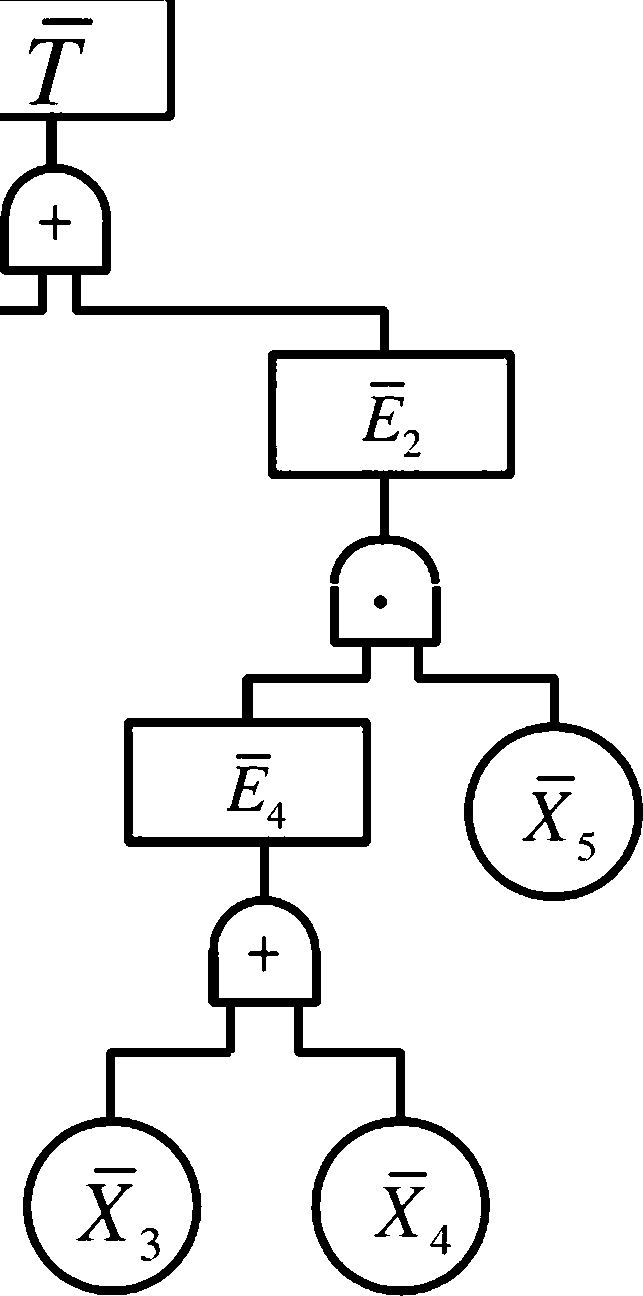
T = E[ + = E頌 Xr + E「X,
i 匕 I 。
顼* *+区+知瓦 ɪ I
=又•兄• X + X •兄+又• X
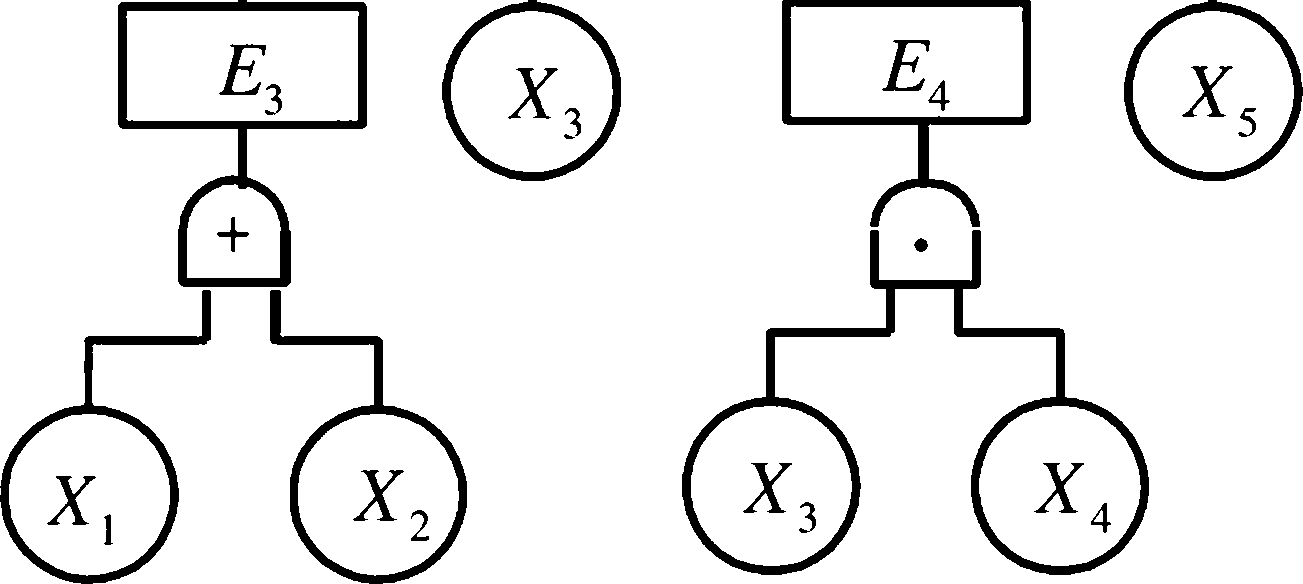
g ={x“X2,X3};4 ={X3,Xs};4 ={X5,xj
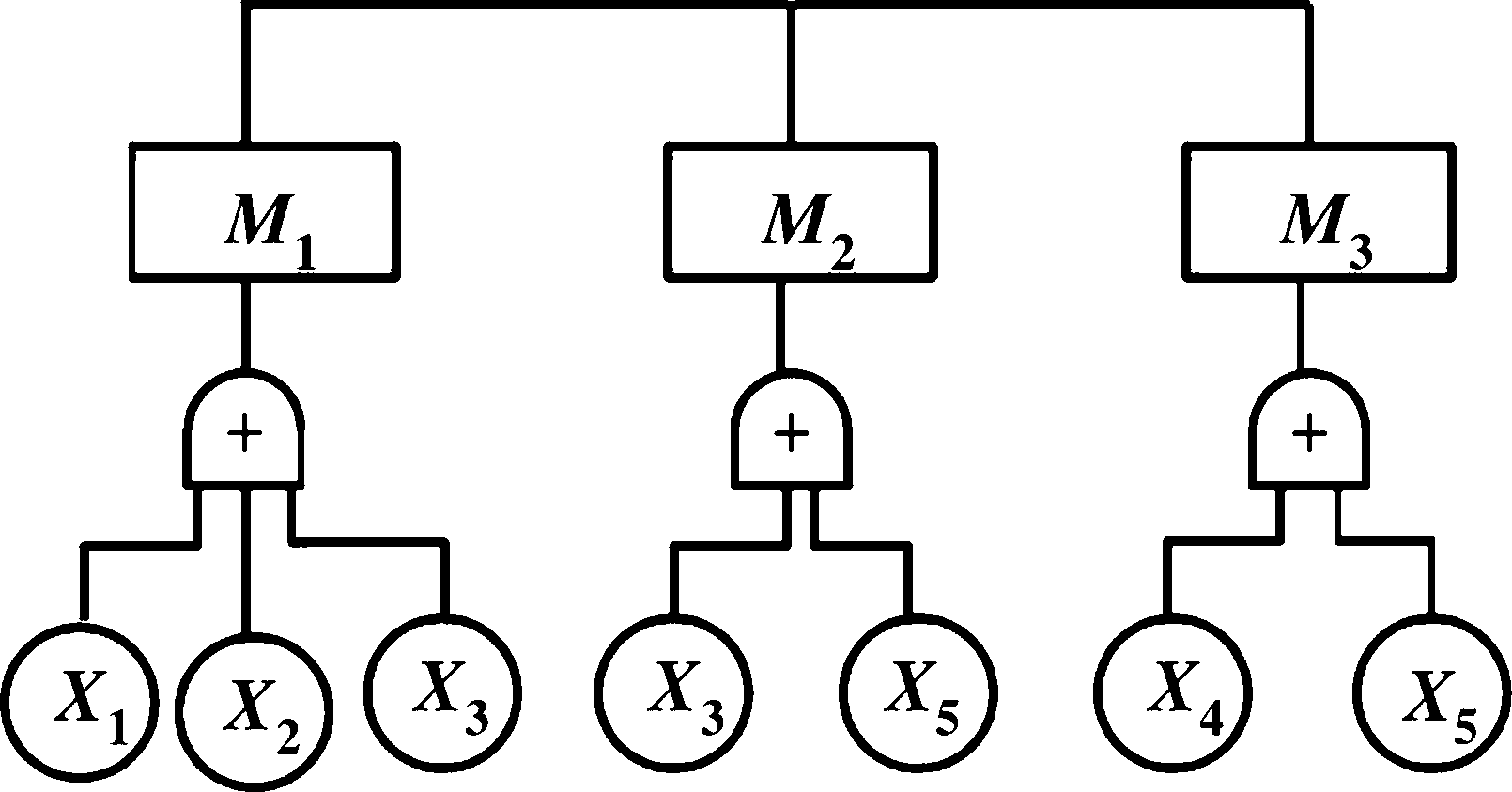
t =(x1 + x2 + X3). (X3 + X5)(X4+X5)
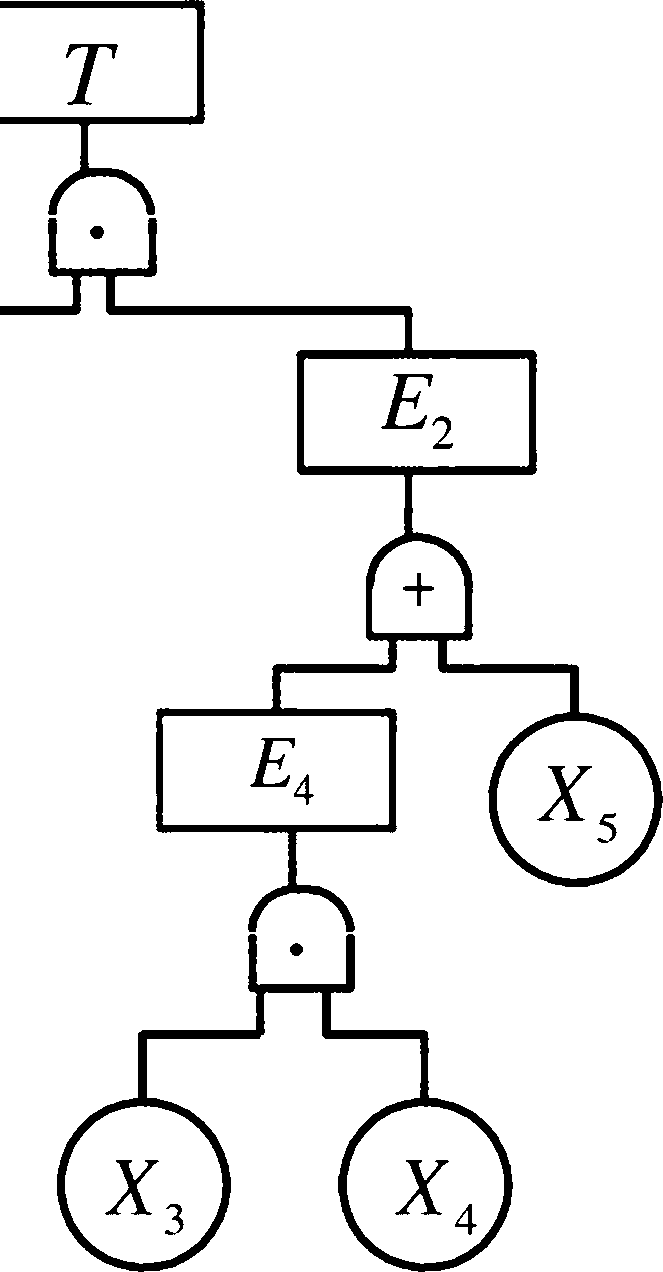
用最小径集表 示的事故树
用最小割集化 简事故树
88
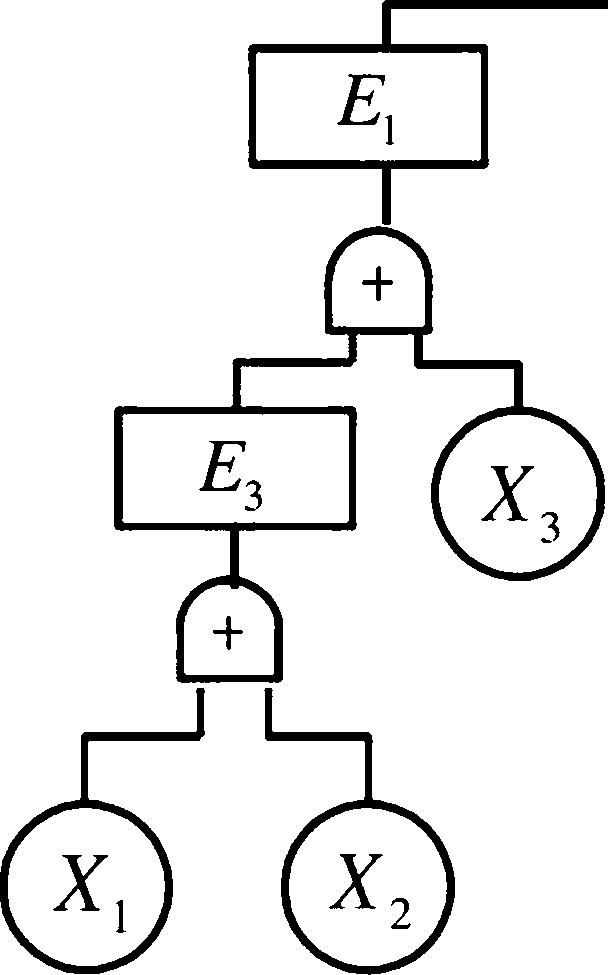
the&2*3+x3)(e4+x5) A(m+X2) + X3」(x3・x4+X5) H(m+X2 + X3)(x3・x4 + X5) H X- • F m+F •撰• m+F F • X4
■ 卜 f J (w (w +m・xn+XM
■ 。 卜 。 。 。
hx-.x=x4 + x\x=x4 + xq・x4
■ 卜 。 (w +m・xn+XM
■ 。 卜 。 。 。
HX-.X=X4 + (1 + X2)XQ・X4 + X-・X5 + X=X5 + X=X M+XM3・x4+m*+x2・x5 + x3* H F • X4+Xm5+F •?<
® ®® ®® ® ® ®
三、基本事件的结构重要度分析
①结构重要度分析就是不考虑基本事件发生的概 率是多少,仅从事故树结构上分析各基本事件
■ 的发生对顶上事件发生的影响程度。
②事故树是由众多基本事件构成的,这些基本事
件对顶上事件均产生影响,但影响程度是不同 的,在制定安全防范措施时必须有个先后次序, 轻重缓急,以便使系统达到经济、有效、安全 的目的。
③结构重要度分析虽然是一种定性分析方法,但
在目前缺乏定量分析数据的情况下,这种分析 是很重要的。
④ 结构重要度分析方法有两种(分析内容):一 种是计算出各基本事件的结构重要度系数,按 系数由大到小排列各基本事件的重要顺序;另 一种是用最小割集和最小径集近似判断各基本 事件的结构重要度的大小,并排列次序。
⑤ 结构重要度系数的求法。
假设某事故树有几个基本事件,每个基本的状 态都有两种:
1「表示基本事件状态发生
表示基本事件状态不发生
■已知顶上事件是基本事件的状态函数, 顶上事件的状态用(P表示,
(p(X) =(P (X” X2, X3,……Xn)则(p
(X)也有两种状态:
「1表示顶上事件状态发生
(p (X)= <
表示顶上事件状态不发生
(P (X)叫做事故树结构函数
■在其他基本事件状态都不变的情况下,基本事件 為的状态从0变到1,顶上事件的状态变化有以下 三种情况:
(1)(p(0卩 X)=0 —(p di,x)=o
则(p (li,X) -(p (Oj, x)=o
不管基本事件是否发生,顶上事件都不发生;
(2)(p (Q, X) =0 —(p(L,X) =1 则(p (Ij, X) -(p (θj, X) =1
顶上事件状态随基本事件状态的变化而变化;
(3)(p (0卩 X) =l^(p(L,X) =1
则(p (lj, X) -9 (Oj, X) =0
不管基本事件是否发生,顶上事件都发生。

|
ɪɪ |
ɪ |
ɪɜ |
她,Xj) |
|
ɪ |
0 |
~6~ |
0 |
|
ɪ |
0 |
] | |
|
1 |
1 |
~o~ |
0 |
|
1 |
1 |
i |
1 |
|
ɪ |
ɪ |
ɪ | |
|
0 |
0 |
0 |
0 |
|
ɪ |
0 |
1 |
0 |
|
ɪ |
1 |
~0~ |
0 |
|
0 |
1 |
1 |
0 |
■上述三种情况,只有第二种情况是基本 事件%不发生,顶上事件就不发生;基 本事件%发生,顶上事件也发生。这说 明%基本事件对事故发生起着重要作用, 这种情况越多,Xj的重要性就越大。
II
El ʃɪ
对有〃个基本事件构成的事故树,"个基本事件 I两种状态的组合数为211个。把其中—个事件%作 *为变化对象(从0变到1),其他基本事件的从态 保持不变的对照组共有2心个。在这些对照组中 属于第二种情况(q)(I., X) -9 (Oi,X) =1 ) 所占的比例即是*基本事件的结构重要度系数, 用L(i)表示,可以用下式计算:
/①(疔 £ [S(L, X)- 她.,X)]
|
ɪɪ |
ɪ |
ɪɜ |
O(L,Xj) |
|
ɪ |
0 |
~0~ |
0 |
|
ɪ |
0 |
] | |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
ɪ |
ɪ |
¢0,xj | |
|
0 |
0 |
0 |
0 |
|
ɪ |
0 |
1 |
0 |
|
ɪ |
1 |
~0~ |
0 |
|
0 |
1 |
1 |
0 |
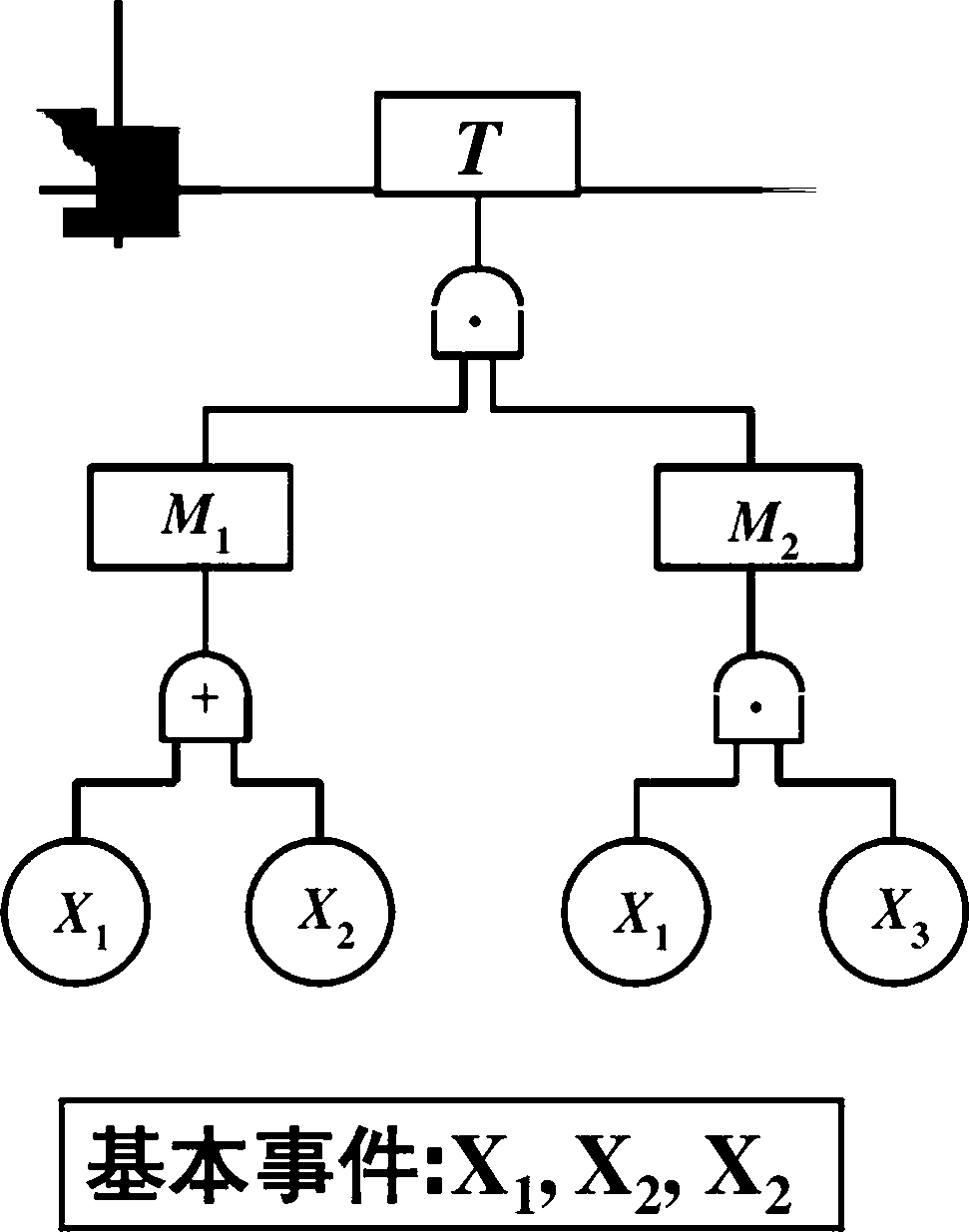
F举例P47,以计算%的结构重要度系数为例
P47图2—13事故树,有4个基本事件
基本事件两种状态的组合数为24个 把X]事件作为变化对象(从0变到1),其他 基本事件的状态保持不变的对照组共有2心 个,即23个。
①(1)=名 N[O(L,x)-°(o”x)] = m
设某一事件有化个最小割集,最小割集旦
中含有个基本事件,则基本事件%的
割集重要系数可用下式计算
(I =、,2,3,・・・/)
g例如:
.
/3(1) = —x( 3 3 2
,3(2) = " W
,3(3)=侦—二
例如:某事故树有三个最小割集:* (Xp X4 ) , E2= {X], X3) , E3= {X],
Xc, X5)
2'
+ - + -)=-
=6'押七Z飞
-,/3(5) = -x-=-
用最小割集或最小径集近似判断各基本事件的 结构重要度大小
这种方法虽然精确度比求结构重要度系数法差 一些,但操作简便,因此目前应用较多。用最 小割集或最小径集近似判断结构重要度大小的 方法也有几种,这里只介绍一种方法。就是用 四条原则来判断,四条原则是:
Ui
■ (1)单事件最小割(径)集中基本事件结构重要
例如:某事故树有三个最小径集:P1= (XJ , P2= (X^ X3} , P3= (x4, x5, x6} o 眞一 个最小念集只含有一个基本事件X],按此原则 X1的结构重要度系数最大。
tOT


■ (2)仅出现在同一个最小割(径)集中的
ʃɪ
ɪ 所有基本事件结构重要度相等。
ɪ 例如:上例中P2= {X2, X3),
I<P (2)=印(3)
■ (3)仅出现在基本事件个数相等的若干个
最小割(径)集中的各基本事件结构重 要度依次出现次数而定,出现次数少, 其结构重要度小;出现次数多,其结构 重要度大;出现次数相等,其结构重要 度相等。 ,—— 例如:某事故树有三个最小割集
牛{Xx, x2, x3),
P2= {X1,x3, x4),
P3= {X], X4, X5} o
此事故树有五个基本基本事件,出现 在含有三个基本事件的最小割集中。按此 原则有:
妃1) >妃3)=妃4) >妃2)=妃5)
.两个基本事件出现在基本事件个数不等 的若干个最小割(径)集中,其结构重 要度系数依下列情况而定:
■若它们在各最小割集中重复出现的次数 相等,则在少事件最小割集中出现的基 本事件结构重要度大;
.例如 p1= {Xi,X3},
P2= {Xi,x4),
P3= (X2, X4, X5),
p4= {X2, x5, x6)
则:妃1)>妃2)
■若它们在少事件最小割集中出现次数少,在多 事件最小割集中出现次数多,以及其他更为复 杂的情况,可用下列近似判别式计算:
(0 -1
■ I⑴ ——基本事件Xj结构重要度的近似判断值, /⑴大则七(D也大;
■ XFKj——基本事件Xj属于%最小割(径)集;
■ n{—基本事件Xj所在最小割{径)集中包含基 本事件的个数。
例如:某事故树共有五个最小径集:
g Px= {X19 X3) , P2= {X19 X4}, ɪ P3= {X2, X4, X5} , P4= (x2, x5, x6}
P5= {X2, x6, x7}根据这个原则:
,_ 1 1
1 1 1 _3
,⑵-2^-i + 23-1 + 23-1 — 4
由此可知:/9 (1)>I9 (2)
■利用上述四条原则判断基本事件结构重 J 要度大小时,必须从第一至第四条按顺 ■> 序进行,不能单纯使用近似判别式,否 则会得到错误的结构。
■用最小割集或最小径集判断基本事件结 构重要度顺序其结果应该是一样的。选 用哪一种要视具体情况而定。一般来说, 最小割集和最小径集哪一种数量少就选 那一种,这样包含的基本事件容易比较。
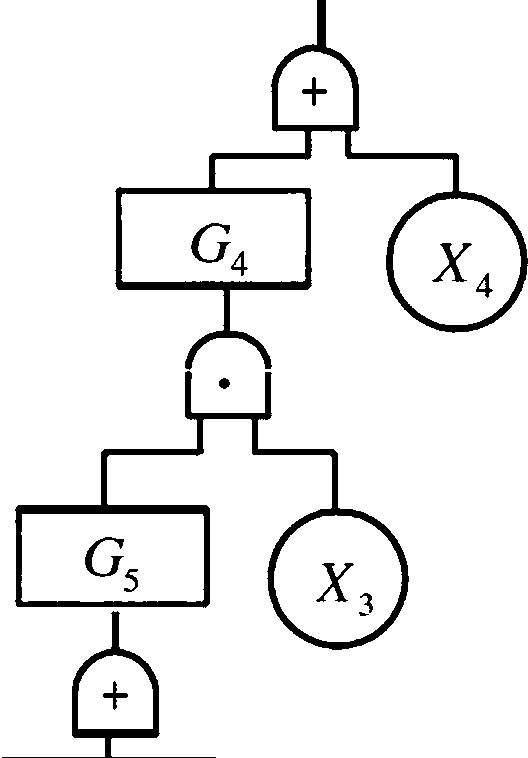
■举例:定性分析
■最小割集为
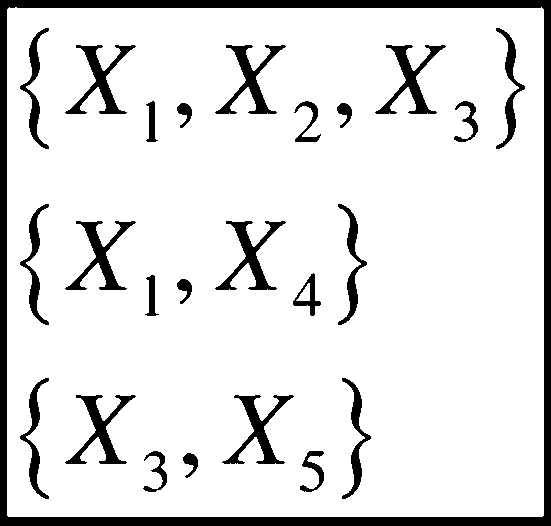
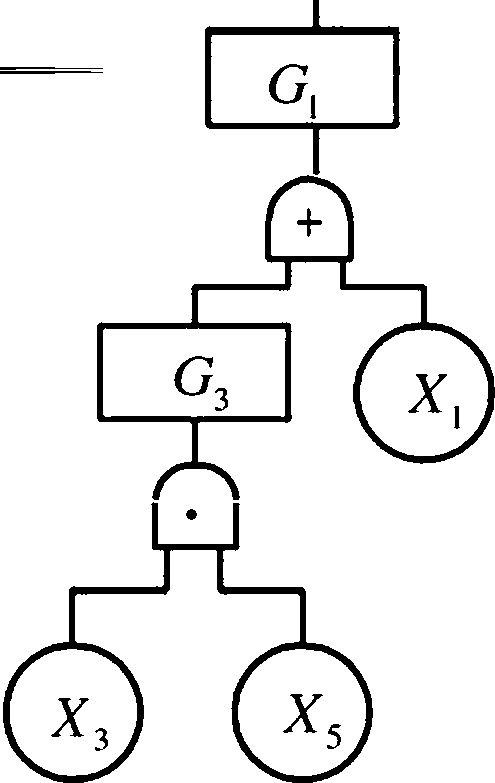
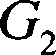
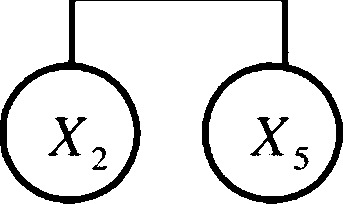
II
II
|
3 |
X— | |
|
II |
II | |
|
2 2 |
2 2 I | |
|
I |
丄 | |
|
+ |
+ | |
|
2 3 I |
I— |
2 3 丄 |
|
II |
II | |
|
4 |
3 |
4 I |
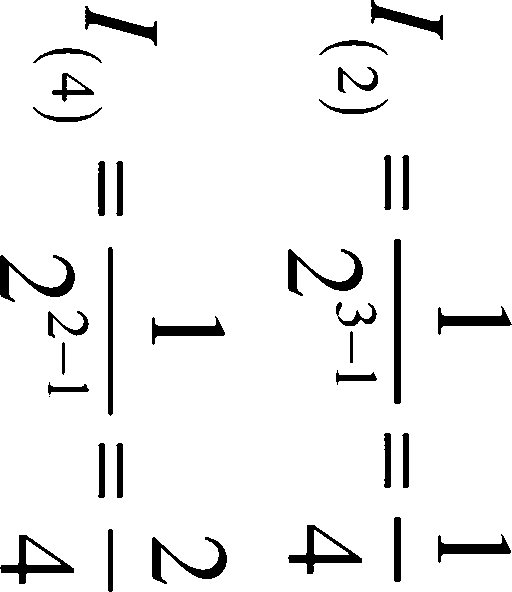
■在这个例子中,近似判断法与精确计算各基 本事件结构重要度系数方法的结果是相同的。
■分析结果说明:仅从事故树结构来看,基本 事件X1和*3对顶上事件发生影响最大,其次 是X4和悬,乂2对顶上事件影响最小。据此, 在制定系统防灾对策时,首先要控制住%和 X3二个危险因素,其次是X4和X5 , *2要根据 情况而定。
□ L?
.基本事件的结构重要度顺序排出后,也可以 作为制定安全检查表、找出日常管理和控制 要点的依据。
最小割集和最小径集在事故树分析中的作用
A. 最小割集表7F系统的危险性。
■由最小割集定义可知,事故树中有一个最小 割集顶上事件发生的可能性就有一种,有几 个最小割集顶上事件发生的可能性就有几种。 事故树中最小割集越多,系统发生事故的途 径越多,因而就越危险。
B. 最小径集表示系统的安全性。
■由最小径集定义可知,事故树中有一个最小 径集,则顶上事件不发生的可能性就有一种, 事故树中最小径集越多,说明控制顶上事件 不发生的方案就越多,系统的安全性就越高。
C.最小割集可直观比较各种故障模式的危险性。
■事故树中有一个最小割集,说明系统就有一种 故障模式。在这些故障模式中,有的只含有1 W 个基本事件,有的含有2个基本事件,还有的 含有3个、4个甚至更多个基本事件。含有1个 基本事件的最小割集,只要1个基本事件发生, 顶上事件就会发生;含有2个基本事件的,必 须2个基本事件同时发生,顶上事件才会发生。 很显然,1个事件发生的概率要比2个事件同时 发生的概率大得多,3个事件同时发生的概率 就更少了。因此,最小割集含有的基本事件越 少,这种故障模式越危险。只含有1个基本事 件的割集最危险。
D.从最小径集可选择控制事故的最佳方案。
■事故树中有一个最小径集,控制顶上事件不发
* 生的方案就有一种。事故树有几个最小径集,
使顶上事件不发生的方案就有几种。在这些方
案中,选择哪一种最好,一般来说,控制少事 件最小径集中的基本事件比控制多个基本事件 省工、省事、经济、有效。当然也有例外,有 时小事件径集中的基本事件由于经济或技术上 的原因,难以控制,这种情况下应选择其他方
案。
E. 利用最小割集和最小径集,可进行结构重要 度分析。
F. 利用最小割集和最小径集可对系统进行定量 分析和评价。
(FAULT TREE QUANTIFICATION)
■ Fault tree analysis is not a quantitative analysis; however, the tree can be quantifled. The most common method of quantiHcation is to assign failure probabilities to each events. Then use the various laws of probability and statistics and solve for the top event.
■事故树的定量分析的任务:在求出各基本事件的发生
概率情况下,计算或估算系统顶上事件的发生概率。
;n
■求出顶上事件发生的概率之后,可与系统安全目标值 进行比较和评价,当计算值超过目标值时,就需要釆 取防范措施,使其降至安全目标以下。
■在进行事故树定量分析时,应满足几个条件:
» ①各基本事件的故障参数或故障率已知,且数 据可靠;
② 在事故树中应完全包括主要故障模式
③ 对全部事件用布尔代数作出正确的描述
■在进行事故树定量计算时,一般做以下几个假 设:
① 基本事件之间相互独立;
② 基本事件和顶事件都只考虑两种状态;
③假定故障分布为指数函数分布。
.基本事件发生概率包括系统单元(部件
或元件)故障概率及人的失误概率等,
在工程计算时,往往用基本事件发生的 频率来代替其概率值。
■ The fault tree is drawn and then the Boolean equations and minimal cut sets are derived for the top event. Probability estimates can be generated from hardware failure data, human error estimation, maintenance frequency, etc. Probability estimates are then assign to the events.
■ Be sure to take into consideration uncertainty limits to your failure data* Through the laws of probability, combine the probabilities to determine the top events
1.系统单元故障概率
ɪ- (1)可修复系统单元故障概率。可修复系统的 单元故障概率定义为:
2 q =----
人+ //
式中:0—单元故障概率;
」单元故障率,指单位时间内故障发生的频率;
卩—单元修复率,指单位时间内元件修复的频率。
■ 一般情况下,单元故障率为:
. Ho
式中:K—综合考虑温度、湿度、振动及其他 条侔影响的修正系数,一般〜10;
扁—单元故障率的实验值,一般可根据实验或 统计求得,等于元件平均故障间隔期的倒数, 即:
MTBF
式中:MTBF——为平均故障间隔期,是指相 邻两次故障间隔期内正常工作的平均时间。
■平均故障间隔期,一般可按下式计算:
1 _ n
MTBF = —£l
n i=i 1
式中:〃—各单元发生故障的总次数;
—第M次到第/次故障间隔时间。
"尊元修复卩一般可根据统计分析用下式求
1
卩=----
MTTR
式中^MTTR为平均修复时间,是指系 统单元出现故障,从开始维修到恢复正 常工作所需的平均时间。
■—般,MTBF>>MTTF,所以人VV^i, 则其故障概率为:
q =-----幻——
人+ /7 卩
(2)不可修复系统的单元故障概率。不可 维修系巍的单元故障概率为:
X— 1 一为
q=l-e
■式中,—为元件的运行时间。
■如果把。一为 按级数展开,略去后面的 高阶无穷小,则可近似为
At
2.人的失误概率
①人的失误是另一种基本事件,系统运行中的
人的失误是导致事故发生的一个重要原因。
②人的失误是指作业者实际完成的功能与系统 所要求的功能之间的偏差。
③人的失误概率是指作业者在一定条件下和规
定时间内完成某项规定功能时出现偏差或失误
nJ
的概率,它表示人的失误可能性大小,因此, 人的失误概率也就是不可靠度。一般根据人的 不可靠度与的人的可靠度互补的规则,获得人 的失误概率。
■影响人失误的因素很复杂,很多专家、 学者对此做过专门研究,提出了不少关 于人的失误概率估算方法,但都不很完 善。现在能被大多数人接受的是1961年 斯温和罗克提出的“人的失误率预测方 法”。这种方法的分析步骤如下:
① 调查被分析者的作业程序;
II
② 把整个程序分解成单个作业;
II
③ 再把每一个作业分解成单个动作;
④根据经验和实验,适当选择每个动作的

可覇度;
⑤用单个动作的可靠度之积表示每个操作
步骤的可靠度。如果各个动作中存在非 独立事件,则用条件概率计算。
⑥ 用各操作步骤可靠度之积表示整个程序 的可靠度;
⑦ 用可靠度之补数(1 •可靠度)表示每个 程序的不可靠度,这就是该程序人的失 误概率。
■ 系统中的功能主要是接受信息
(输入)、处理信息(判断)和操纵控 璽机差臂吏息输出。因此就某一动作而 言’作业善的蠢本可靠度房:
式中:
与输入有关的可靠度;
&2—与判断有关的可靠度;
/?3—与输出有关的可靠度。
■由于受作业条件、作业者自身因素及作
业环境的影响,基本可靠度还会降低。
例如,有研究表明,人的舒适温度一般 是19-22°C,当人在作业时,环境温度
超过27 C时,人体失误概率大约会上升
40% o
.因此,还需要用修正系数K加以修正, 从而得到作业者单个动作的失误概率为ɪ
■ q=k (LR)
■式中:J修正系数
k=a・b・c・d・e;
*一〃—作业时间系数;
力一操作频率系数;
c—危险状况系数;
d一心理、生理条件系数;
e一环境条件系数。
取值范围见表3—13
二、顶上事件发生的概率
1.如果事故树中不含有重复的或相同的基本事
件,各基本事件又都是相互独立的,顶上事件
发生的概率可根据事故树的结构,用下列公式 求得。
■用“与门”连接的顶事件的发生概率为:

用“或门"连接的顶事件的发生概率为:
n
F0) = i-II(1f)
Z = 1

式中:Qi---
2, ......n) o
第Z个基本事件的发生概率(/=1,
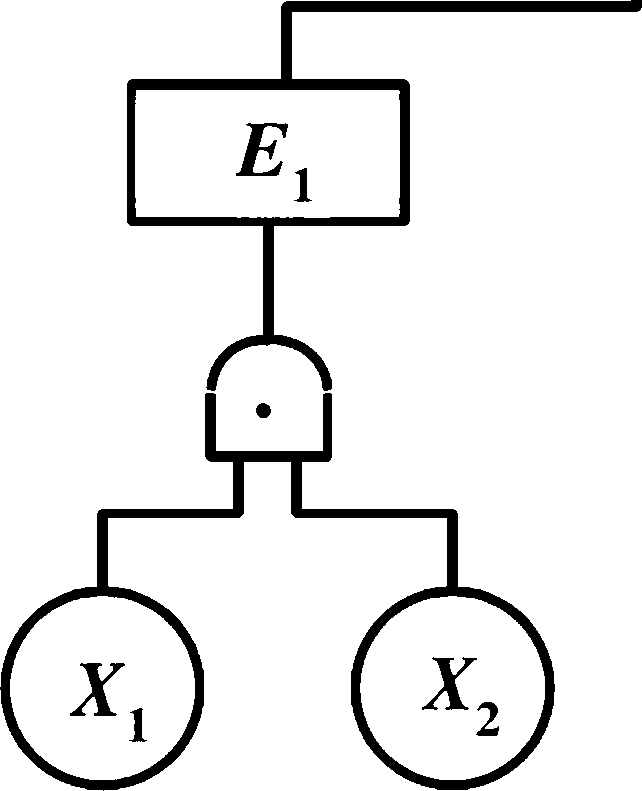
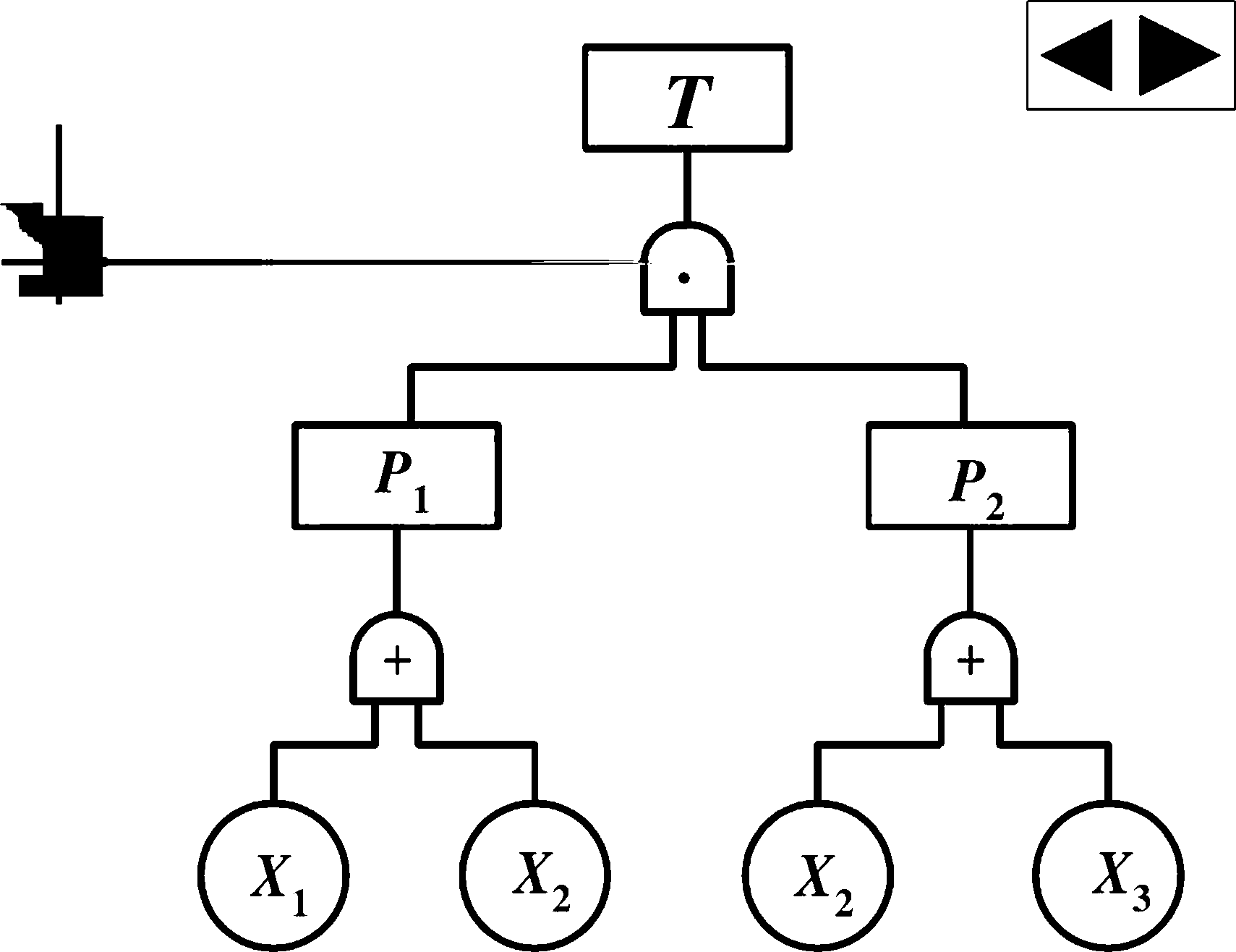
例如:某事故树共有2个最小割集: 已知各基本事件发生的概率为:
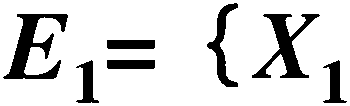
,X2},
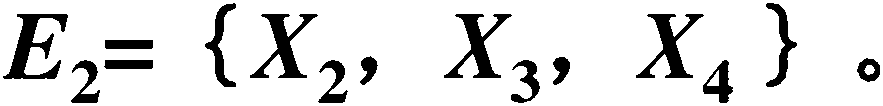
¢1=0.5 ; q2=0.2 ; q3=0.5; q4=0.5; 求顶上事件发生概率?
>
*
n
X2
2
p(t)=i-n(i-已)=1-(1-也)(i-也) /=1
2 3
ɪi-(i-n^)-(i-n^ɔ
i=\ i=l
二1 一(1一型2)・(1 — 020304)
F0)= l —(l — O.5xO.2)・(l — O.2xO.5xO.5) = 0.145
PQ) ɪl-ɑ-0102 一 020304 + 0102020304)
= 0102+020304—01020304
=0.5 x 0.2 + 0.2x0.5 x 0.5 -0.2 x 0.5 x 0.5 x 0.5 = 0.125
2.但当事故树含有重复出现的基本事件时,
或基本事件可能在几个最小割集中重复 出现时,最小割集之间是相交的,这时, 应按以下几种方法计算。
①最小割集法
■事故树可以用其最小割集的等效树来表示。这 时,员上事彳车奪于最爪割集的并至。
■设某事故树有K个最小割集:E]、&2、 Er、…、Ek,则有:
JU旦
r=l
■顶上事件发生概率为:
P(T) = p\\jEr
I r=l
■化简,顶上事件的发生概率为:
尸3) = £卩0•- £ 卩 Qi +•••+(-1/-1 H 么
r=l x^Er \<r<s<k x eeA \e, 厂=1
耳皆u&U号'U切
■式中:r、s、k—最小割集的序号, r<s<k;
基本事件的序号,
l<r<5<fc~~A:个最小割集中第,、s两个割集的组合 顺序;
* E E—属于第,个最小割集的第,个基本事件;
X e£共一属于第尸个或第$个最小割集的第/个基 本事彳牛。5
例如:某事故树共有3个最小割集:试用 *最小割集法计算顶事件的发生的概率。
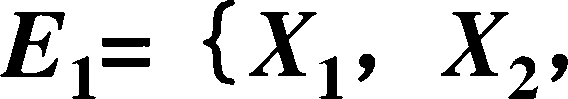
X3 },E2= {xv
x4}
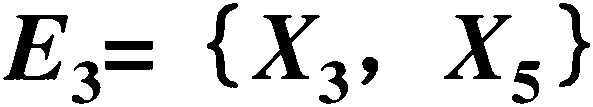
已知各基本事件发生的概率为:
¢1==0.01 ; 02=0・°2; ”3=°,°3; (jr4=0e04 ;
05=0.05
求顶上事件发生概率?
n^- e n "…+㈠〃 r=l x^Er \<r<s<k xi&Er\jEs
fl q,
r=l
glj&Lk …U&
PQ) ~ 010203 + 0104 + 0305
―么么么么—01020305 — 01030405 + 0102^30405
= 0.001904872
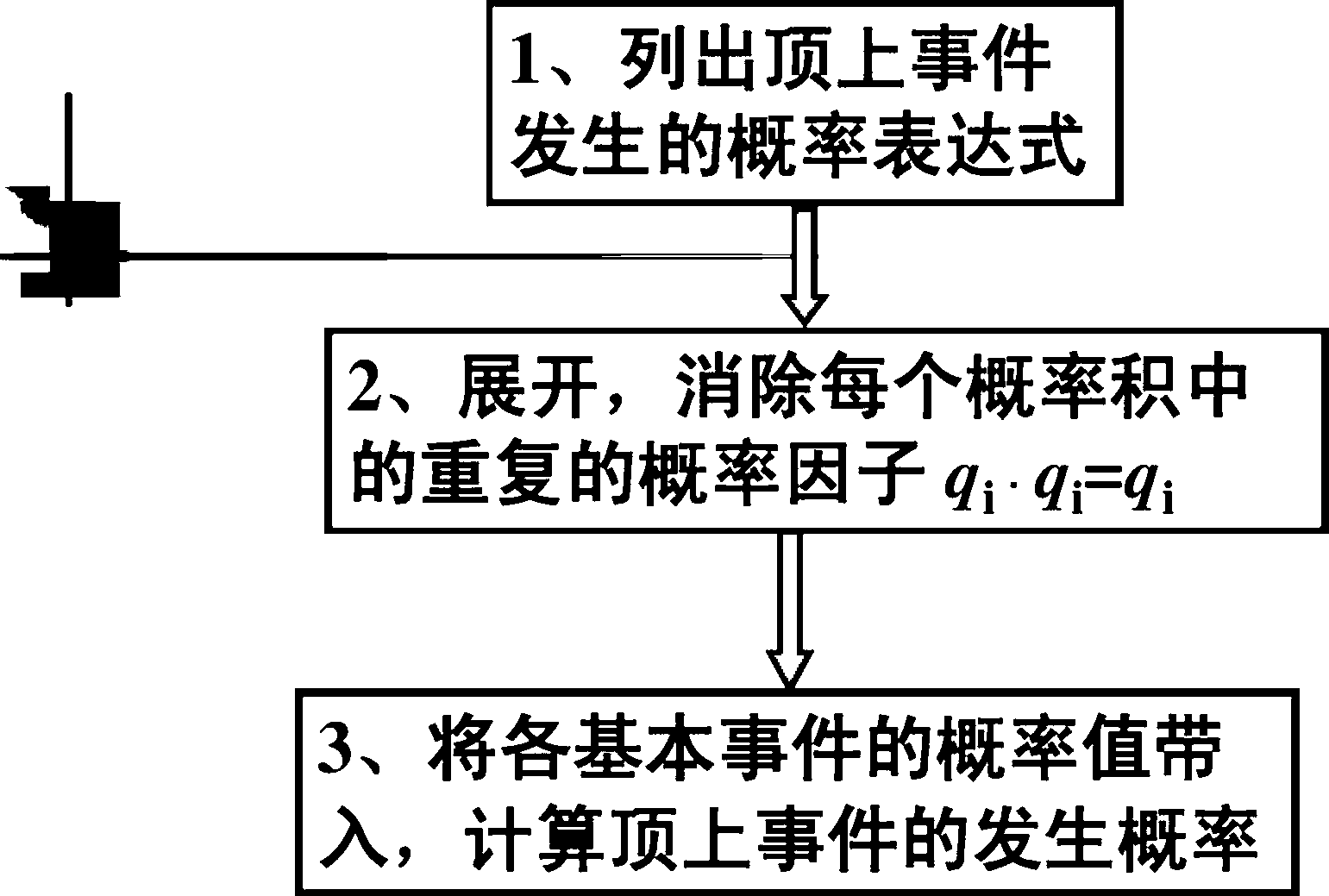

如果各个最小割集中彼此不存在重复的基本事 件,可省略第2步
③最小径集法
■根据最小径集与最小割集的对偶性,利 用最小径集同样可求出顶事件发生的概 率。
■设某事故树有k个最小径集:0、P2.....
4、…、尸k。用Q(r=L 2, ..., k)表 示最小径集不发生的事件,用 表示顶 上事件术发生。
■由最小径集定义可知,只要化个最小径集 中有一个不发生,顶事件就不会发生, 则:
T=\jDr
r=l
1 —F(牛朮
〔r=l .
■故顶上事件发生的概率:
,s)=i-zri(iF)+ £ n(i-^.)--+(-ir n a)
另eRU名U4…U4
r> s—最小径集的序数,rvs;
S最小径集数;
(l-^r)—第Z个基本事件不发生的概率;
X;. Ep,—属于第尸个最小径集的第i个基本事件;
改e Pr U 属于第尸个或第s个最小径集的第i个
基本事件
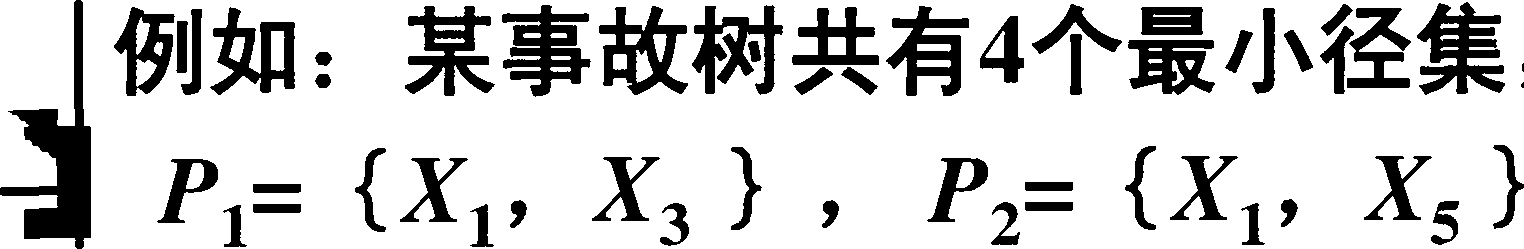
已知各基本事件发生的概率为:
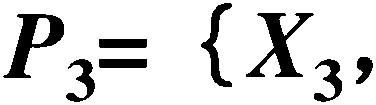
x4}
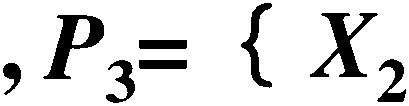
,X4,
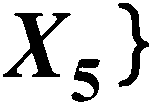
饥=0・01 ; 02=°・°2 ; 03=°・°3 ; 04=°・°4 ; 05=0.05
试用最小径集法求顶上事件发生概率?
冲=1-如(1-0)+ l n fɪ I)
r=I x&Pf \<r<s<k xiePr(JPs r=l
誓gU%U&・・U4
F(T) = ]_[(】_ 01 )(1-03)+(】_01 )(1 —05)+(1一 03)(1-04)
+ (1 - 02)(1 — 04)(1 — 05)] +(1 — 01)(1 — 03)(1 — 05)+(1 — 01)(1 — 03)(1 一 04)
+ (1 — 01 )(ɪ — 02 )(ɪ- 03)(1 - 04)(1 - 05)+(1 - 01)(1 - 05)(1 - 03)(1 - 04)
+(1 - 01 )(1 - 02 )(ɪ — 04)(1 - 05)+(1 - 02)(1 - 03)(1 - 04)(1 - 05)
一[(1 一 0 )(ɪ — 03 )(1 — 04)(1 — 05)+(1 — 01)(1 — 02 )(ɪ — 03 )(ɪ 一 04)(1 - 05)
+(1-01)(1-02)(1一03)(1一 04)(1一 05)]+(1一01)(1一 02)(1一03)(1一04)(1一05)
1>列出定上事件 发生的概率表达式
2、展开,消除每个概率积中的重
复的概率因子(1*)=1%
3、将各基本事件的概率值带
EI ʃɪ
入,计算顶上事件的发生概率
如果各个最小径集中彼此不存在重复的基本事 件,可省略第2步
例如:某事故树共有2个最小径集:0= {Xi,X2}, P2= {X2, X3} 0已知各基本事件发生的概率为: qi=0.5; 02=。・2; %=。・5;求顶上事件发生概率?
P(T) = Pp「Pp2
-[1 — Q —01)(1 —02 — (1 — 02 )(1 —03)]
二(01 + 02 一 0102 )02 + 03 一 0203)
=0102 + 0103 一 010203 + 0202 + 0203 一
—020203 —010202 —010203 +01020203
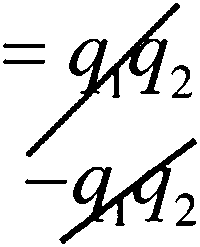
+ 0103 一 010203 + 02 -橢3
~ 010203 + 010203
二0103 一010203 +02
=0.5x 0.5-0.5x0.2x0.5+ 0.2 = 0.4
.基本事件的重要度:一个基本事件对顶 上事件发生的影响大小。
.基本事件的结构重要度分析只是按事故 树的结构分析各基本事件对顶事件的影 响程度,所以,还应考虑各基本事件发 生概率对顶事件发生概率的影响,即对 事故树进行概聿重要度分析。
=1 4、
■事故树的概率重要度分析是依靠各基 本事件的概率重要度系数大小进行定 量分析。所谓概率重要度分析,它表 示第,个基本事件发生的概率的变化引 起顶事件发生概率变化的程度。由于 顶上事件发生概率函数是〃个基本事 件发生概率的多重线性函数,所以, 对自变量%求一次偏导,即可得到该 基本事件的概率重要度系数。
ʃɪ
・Xj基本事件的概率重要度系数:
Ig(0 =
dP(T)
■式中:P (T)一顶事件发生的概率;
@ 一第,个基本事件的发生概率。
■利用上式求出各基本事件的概率重要度 系数,可确定降低哪个基本事件的概率 能迅速有效地降低顶事件的发生概率。
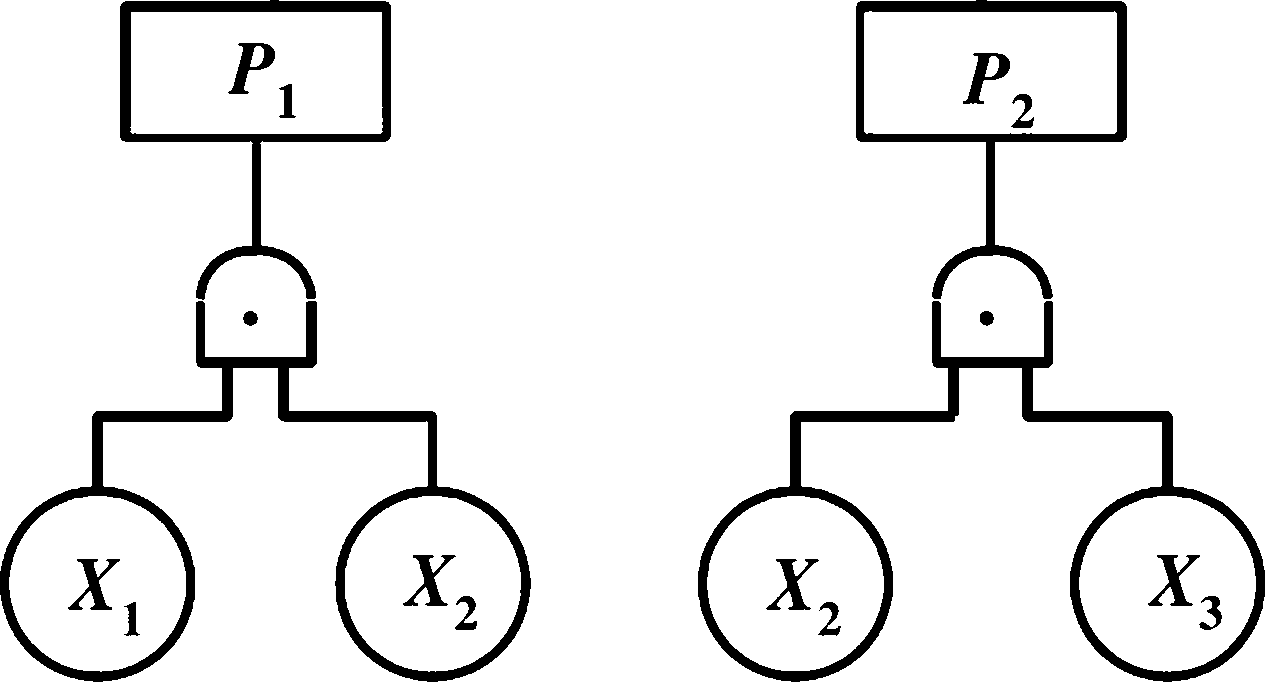
例如:某事故树共有2个最小割集:E]= {X19 X2}, e2= {X2f X3} o已知各基本事件发生的概率为: qi=0.4; 02=。・2; %=。・3;排列各基本事件的概率重 要度,
P(T) = 0102 +0203 一 010203 =°・116
/ m _ 0P(T) _ _nlA
/ (1) _ —- _ 02 - 0203 — 0・16
为]
4(2)>//1)>//3)
/(2) = —ɪ = 0i + 03 — 0103 = 0.49
为2
dP(T)
Ig (ɔ) = = 02 _ 0102 = 0. 12
为3
*—1 TT
I
I、基本事件的关键重要度(临界重要度)
■当各基本事件发生概率不等时,一般情
况下,改变概率大的基本事件比改变概
率小的基本事件容易,但基本事件的概
率重要度系数并未反映这一事实,因而 它不能从本质上反映各基本事件在事故 树中的重要程度。
■关键重要度分析,它表示第,个基本事件 发生概率的变化率引起顶事件概率的变 化率,因此,它比概率重要度更合理更 具有实际意义。
^P(T)/p(T)
r(i)= lim r` 宀
Qi r ʌ/^(r) =———• lim -----
p(T) Agf △%
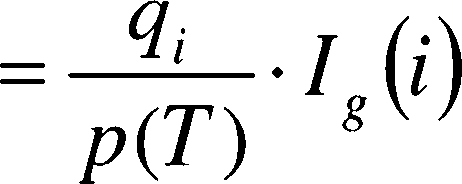
■式中—第i个基本事件的关键重要度系数;
/ (;)一第,个基本事件的概率重要度系数; P'(T)一顶事件发生的概率;
q.—第i个基本事件发生概率。
例如:某事故树共有2个最小割集:E]= {X19 X2},
e2= {X29 x3} o已知各基本事件发生的概率为:
91=0.4;必=。・2; 03=。・3;排列各基本事件的关键重 #■要度,
F0) = 0.116;七⑴= 0.16; I (2) = 0.49; / J3) = 0.12
/c(l)= ML/ (l) = Ef_x0.16 = 0.552
& P(T) g 0.116
r\ ɔ
/: (2) = ʃ (2) = x 049 = 0.845
八 P(T) 8 0.116
r (3) = M-九⑴=X 0.12 = 0.310 g F0) g 0.116
/;(2)>/;(1)>/;(3)
159